Neural vector embeddings
Hyperdimensional Computing, Vector Symbolic Architectures, Holographic Reduced Representations
December 20, 2017 — May 22, 2025
Suspiciously similar content
Representations of complicated spaces by vectors which preserve semantic information.
Warning: this is not my current area, and it is a rapidly moving one. Treat notes here with caution; many are outdated.
Feature construction for inconvenient data; made famous by word embeddings such as word2vec which ended up being both useful and surprisingly semantic.1 Vector embeddings are now even more famous for LLMs, and indeed, reality itself.
1 Platonic Representation Hypothesis
Are the semantics of embeddings for different models or modalities represented in a common “Platonic” space which is universal in some sense (Huh et al. 2024)? If so, should we care?
I confess I struggle to see how to make this concrete enough to produce testable hypotheses, but that’s probably because I haven’t read enough of the literature. Here’s something that might have made progress:
- jack morris “excited to finally share on arxiv what we’ve known for a while now: All Embedding Models Learn The Same Thing embeddings from different models are SO similar that we can map between them based on structure alone. without *any* paired data. feels like magic, but it’s real:🧵” (Jha et al. 2025)
My colleague Pascal Hirsch mentions the hypothesis that
This should also apply to the embeddings people have in their brains, referring to this fascinating recent Google paper (Goldstein2025Unified?)
[…] neural activity in the human brain aligns linearly with the internal contextual embeddings of speech and language within LLMs as they process everyday conversations.
2 Tutorials
Vicki Boykis’ series What are Embeddings?
Rutger Ruizendaal wrote a tutorial on learning embedding layers.
Technical survey: Kleyko et al. (2022) cites back to the year 2000.
3 History and background
Baby’s first embedding! As invented by (Bengio et al. 2003) and popularised/refined by Mikolov and Dean at Google, the skip-gram semantic vector spaces is a useful way to define String distances for natural language this season.
Christopher Olah discusses RNN embeddings from a neural network perspective with diagrams and commends (Bengio et al. 2003) for a rationale.
Sanjeev Arora’s semantic word embeddings has an explanation of skipgrammish methods:
In all methods, the word vector is a succinct representation of the distribution of other words around this word. That this suffices to capture meaning is asserted by Firth’s hypothesis from 1957, “You shall know a word by the company it keeps.” To give an example, if I ask you to think of a word that tends to co-occur with cow, drink, babies, calcium, you would immediately answer: milk.
[…] Firth’s hypothesis does imply a very simple word embedding, albeit a very high-dimensional one.
Embedding 1: Suppose the dictionary has N distinct words (in practice, N=100,000). Take a very large text corpus (e.g., Wikipedia) and let Count5(w1,w2) be the number of times w1 and w2 occur within a distance 5 of each other in the corpus. Then the word embedding for a word w is a vector of dimension N, with one coordinate for each dictionary word. The coordinate corresponding to word w2 is Count5(w,w2). (Variants of this method involve considering cooccurence of w with various phrases or n-tuples.)
The obvious problem with Embedding 1 is that it uses extremely high-dimensional vectors. How can we compress them?
Embedding 2: Do dimension reduction by taking the rank-300 singular value decomposition (SVD) of the above vectors.
Using SVD to do dimension reduction seems an obvious idea these days but it actually is not. After all, it is unclear a priori why the above N×N matrix of cooccurance counts should be close to a rank-300 matrix. That this is the case was empirically discovered in the paper on Latent Semantic Indexing or LSI.
-
For both descriptions below, we assume that the current word in a sentence is \(w_i.\)
CBOW: The input to the model could be \(w_{i-2}, w_{i-1}, w_{i+1}, w_{i+2},\) the preceding and following words of the current word we are at. The output of the neural network will be \(w_i\). Hence you can think of the task as “predicting the word given its context”. Note that the number of words we use depends on your setting for the window size.
Skip-gram: The input to the model is \(w_i\), and the output could be \(w_{i-1}, w_{i-2}, w_{i+1}, w_{i+2}\). So the task here is “predicting the context given a word”. Also, the context is not limited to its immediate context, training instances can be created by skipping a constant number of words in its context, so for example, \(w_{i-3}, w_{i-4}, w_{i+3}, w_{i+4}\), hence the name skip-gram. Note that the window size determines how far forward and backward to look for context words to predict.
According to Mikolov:
Skip-gram: works well with small amount of the training data, represents well even rare words or phrases.
CBOW: several times faster to train than the skip-gram, slightly better accuracy for the frequent words.
This can get even a bit more complicated if you consider that there are two different ways how to train the models: the normalized hierarchical softmax, and the un-normalized negative sampling. Both work quite differently.
which makes sense since with skip gram, you can create a lot more training instances from limited amount of data, and for CBOW, you will need more since you are conditioning on context, which can get exponentially huge.
Jeff Dean’s CIKM Keynote. (that’s “Conference on Information and Knowledge Management” to you and me.)
“Embedding vectors trained for the language modelling task have very interesting properties (especially the skip-gram model)”
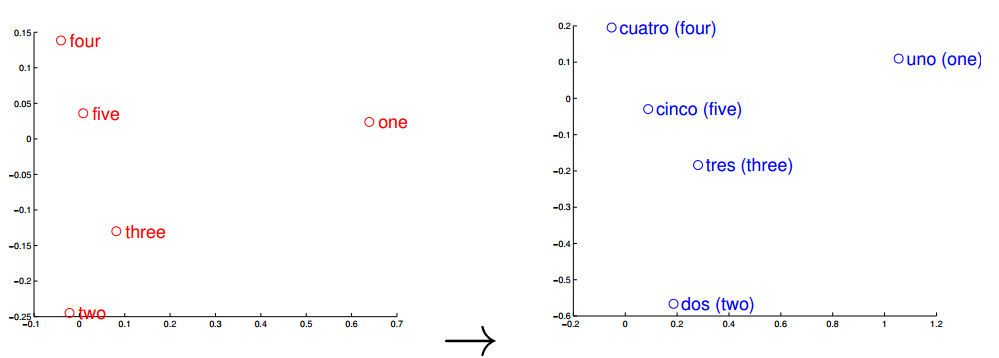
\[ E(\text{hotter}) - E(\text{hot}) &≈ E(\text{bigger}) - E(\text{big}) \\ E(\text{Rome}) - E(\text{Italy}) &≈ E(\text{Berlin}) - E(\text{Germany}) \]
“Skip-gram model w/ 640 dimensions trained on 6B words of news text achieves 57% accuracy for analogy-solving test set.”
Sanjeev Arora explains that, more than that, the skip gram vectors for polysemic words are a weighted sum of their constituent meanings.
-
We describe an approach for unsupervised learning of a generic, distributed sentence encoder. Using the continuity of text from books, we train an encoder/decoder model that tries to reconstruct the surrounding sentences of an encoded passage. Sentences that share semantic and syntactic properties are thus mapped to similar vector representations. […] The end result is an off-the-shelf encoder that can produce highly generic sentence representations that are robust and perform well in practice
Graph formulations, e.g. David McAllester, Deep Meaning Beyond Thought Vectors:
I want to complain at this point that you can’t cram the meaning of a bleeping sentence into a bleeping sequence of vectors. The graph structures on the positions in the sentence used in the above models should be exposed to the user of the semantic representation. I would take the position that the meaning should be an embedded knowledge graph — a graph on embedded entity nodes and typed relations (edges) between them. A node representing an event can be connected through edges to entities that fill the semantic roles of the event type
4 Embedding vector databases
Related: learnable indices. See vector databases.
5 Misc
Entity embeddings of categorical variables (code):
We map categorical variables in a function approximation problem into Euclidean spaces, which are the entity embeddings of the categorical variables. The mapping is learned by a neural network during the standard supervised training process. Entity embedding not only reduces memory usage and speeds up neural networks compared with one-hot encoding, but more importantly by mapping similar values close to each other in the embedding space it reveals the intrinsic properties of the categorical variables. We applied it successfully in a recent Kaggle competition and were able to reach the third position with relative simple features. We further demonstrate in this paper that entity embedding helps the neural network to generalize better when the data is sparse and statistics is unknown. Thus it is especially useful for datasets with lots of high cardinality features, where other methods tend to overfit. We also demonstrate that the embeddings obtained from the trained neural network boost the performance of all tested machine learning methods considerably when used as the input features instead. As entity embedding defines a distance measure for categorical variables it can be used for visualising categorical data and for data clustering.
6 Software
-
This tool provides an efficient implementation of the continuous bag-of-words and skip-gram architectures for computing vector representations of words. These representations can be subsequently used in many natural language processing applications and for further research.”
-
fastText is a library for efficient learning of word representations and sentence classification.