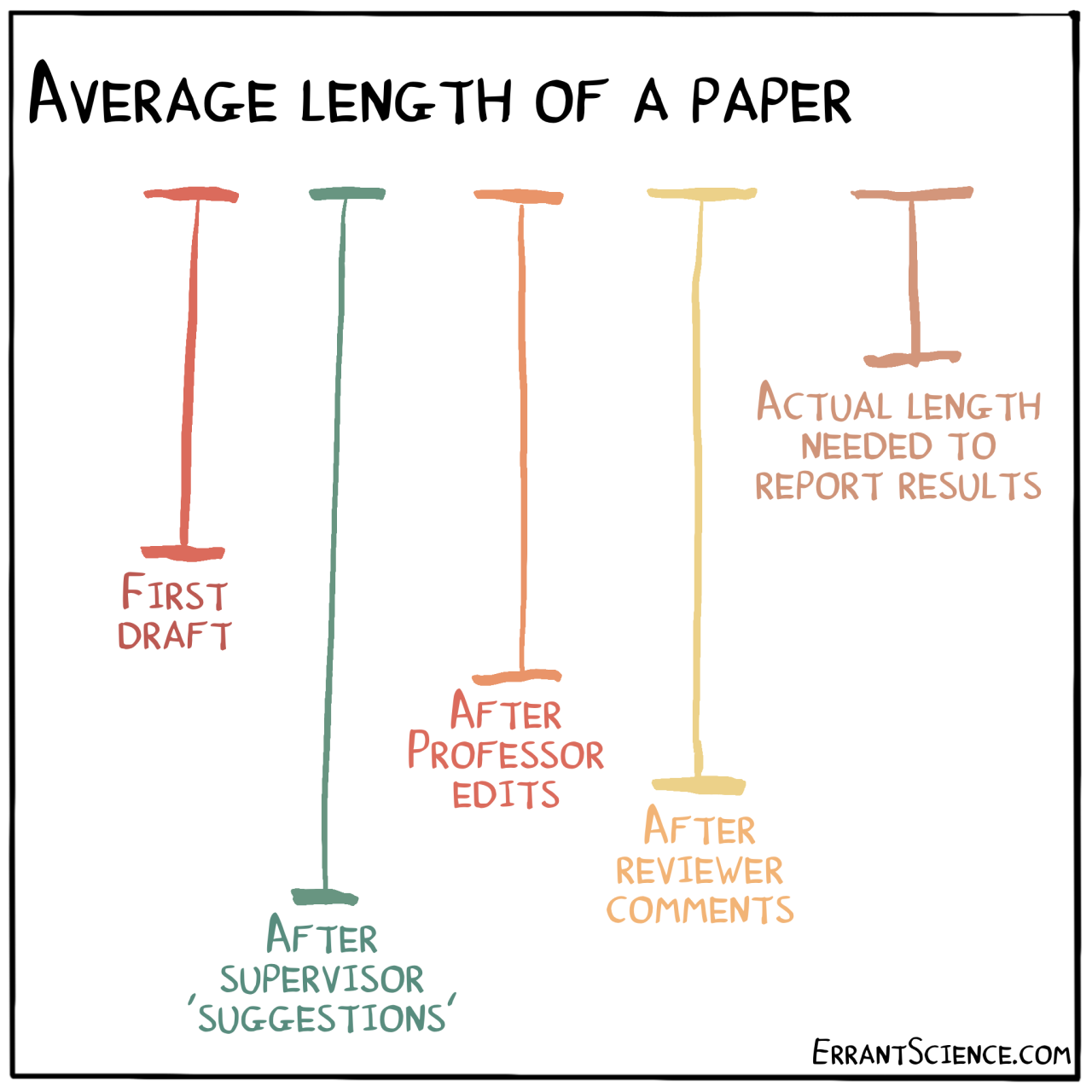
Scientific writing
In which tips are given for the projection of status through nominal phrases and passive voice
2014-12-31 — 2026-01-20
Wherein the rituals of academese are examined and the tradeoff between clarity and status signalling is described, with attention paid to mathematical notation and editorial incentives.
Scientific writing is frequently terrible. As an undergraduate, I studied linguistics. The psycholinguistics content focused on questions like how hard, relatively, a subordinate passive voice is for our brains to process. We quantified that by, for example, measuring how long people paused to understand a passive phrasing compared with an active one. Of course, the essays on these themes had to be written in hard-to-parse scientific style — subordinate clauses, passive voice, and other constructions that we knew made our essays measurably harder to understand.
Why do we do this to ourselves? Possibly because writing is just plain hard, harder in our second language (and scientists tend not to be writing in their mother language), and possibly because a shadowy conspiracy of lecturers aims to create demand for paid educational delivery, such as lectures, where they explain in person what they obfuscated in books. The academic elites, that is, would be in the pocket of Big Talk.
Or maybe it’s because our graduate committee feels they need to give us some feedback, and if they don’t understand our writing they may at least tell us to write more defensively and more pretentiously.
Can we do better (i.e. more beautiful, more comprehensible) while still using enough appropriately rococo status signifiers to get our work published? I’m especially interested in good mathematical style, but academic style in general would also be useful to know.
Yes, mostly. Good academic writing, it seems to me, is about finding a compromise between my aesthetic preferences and the academic status dialect. While I will never get to write a paper the same way I would explain it in person, I can at least avoid some of the bullshit and still be publishable. Put another way, there is a comprehensible style hidden within the status-signaling academese dialect. In public science communication, I can probably aim for my actual preferred style.
It might be good at this point to distinguish several possible styles of writing that I might like to be good at:
Journal-style prose, which has a cloistered academic tone (passive voice, etc.) that’s necessarily constrained, but can be done better or worse within its constraints
Public science communication, where I can use certain forbidden words (e.g. “I”) but often must presume less specialist knowledge from my audience.
Peer, or educational science communication, wherein I can use specialist jargon plus whatever language I need to motivate intuition in my listener.
Inger Mewburn hates conventional academic style:
Academic writing, as a genre, is ritualised, peculiar, archaic and does almost as much to hide knowledge as it does to share it. Mastering academic writing is just as much about signalling you are the member of an ‘in-group’ as it is about conveying ideas.
Don’t believe me? Look at how we use commas.
Commas help you create longer sentences that still make sense. Without commas, you have Parataxis. Parataxis is Plain English. Just one sentence. Followed by another sentence. Parataxis is direct. Your sentences are short.
Perhaps too short?
When you have too many commas you create hypotaxis: the use of clause after subordinate clause, which creates sentences of deeply satisfying complexity, that, even while you might get lost a little between the commas, reassure the reader that an academic of sober-minded, careful, disposition is tapping away at the keyboard crafting very, very polite sentences which, because of those glorious clauses and subordinate clauses, will make you feel like you’re eating dry toast. You’re on safe ground with all that hypotactic fun, believe me, because it’s impossible to be too enthusiastic, or too rude, about anything when you write this way. It’s no wonder, since academics love being passive aggressive, …that most ‘serious’ writing is full of it.
Thomas Basbøll counters Mewburn’s claim about in-group signalling by extolling the virtues of a productive group:
This, then, is my advice to doctoral students and early career researchers. Spend some time looking for a group of people you like writing for and just go ahead and enjoy it for a few hours every week. (I recommend at least two and a half hours and at most fifteen.) This will all be happening within you, in your heart and mind, so you are in control of the moment. Keep the mood warm and collegial. Don’t spend a lot of time writing for readers you don’t like, or readers you fear, or don’t respect, or feel humiliated by. Spend most of your writing time among your peers. Enjoy their company.
From both of these, we can take a recommendation for awareness of context.
To meet the Key Performance Indicators of Australian research, we generally churn out endless stylized academese to get published as often and as quickly as possible, without pausing to make it comprehensible to the public or even to other researchers who aren’t close enough to our field to be gatekeepers. The goal becomes to be just comprehensible enough not to annoy good reviewers, and maybe just incomprehensible enough to intimidate bad reviewers into accepting our work.
We could, nonetheless, be a little better off, I feel, by tithing a small amount of effort to less abhorrent journal submissions. Also, we could advocate for a system that permits this.
I can also complain to other researchers, I suppose.
OK, but how to do better within the constraints we have? There’s no shortage of advice about that. Too much, even. Advice alone won’t fix perverse incentives. Nonetheless, advice is a necessary part of the solution. Maybe at some point I’ll have time to triage these resources better and find out which ones, for example, have evidential support rather than being the groundless mumblings of latter-day prescriptive grammarians. For now: a fountain! A cornucopia! A jungle of verbiage on the topic of how to omit needless words.
1 Actual advice
J.S. Milne, tips for authors:
If you write clearly, then your readers may understand your mathematics and conclude that it isn’t profound. Worse, a referee may find your errors. Here are some tips for avoiding these awful possibilities.
Henning Schulzrinne, Writing technical articles
A good research paper has a clear statement of the problem the paper is addressing, the proposed solution(s), and results achieved. It describes clearly what has been done before on the problem, and what is new.
The goal of a paper is to describe novel technical results. […] A paper should focus on
- describing the results in sufficient detail to establish their validity;
- identifying the novel aspects of the results, i.e., what new knowledge is reported and what makes it non-obvious;
- identifying the significance of the results: what improvements and impact do they suggest.
The author also quotes Craig Partridge:
One goal of the paper is to ensure that the next person who designs a system like yours doesn’t make the same mistakes and takes advantage of some of your best solutions. So make sure that the hard problems (and their solutions) are discussed and the non-obvious mistakes (and how to avoid them) are discussed.
Let’s just imagine if that happened on a regular basis.
Public Library of Science Writing Center:
A collection of free, practical guides and hands-on resources for authors looking to improve their scientific publishing skillset.
Simon Peyton Jones’ pointers to useful advice from his seminar on how to write a paper.
The Navigators Research Book of Style is a slide deck from the Navigators research group at the University of Lisbon. It covers choosing a research topic, doing research, and writing and submitting a paper.
Research tips (including how to do research, how to write and present a paper, how to design a poster, how to review, etc.), by Sylvia Miksch.
Notes on presenting theses, edited by Aaron Sloman, give useful guidelines and ideas for PhD students writing their thesis.
Chris O’Leary’s essays about writing an “elevator pitch”. This material, especially the list of attributes on the “Elevator pitch 101” page, is very relevant to writing a good grant proposal.
A scrutiny of the abstract by Kenneth Landes in Geological Notes. These short notes give guidance on writing the abstract of your paper.
Gian-Carlo Rota’s excellent talk Ten lessons I wish I had been taught, which, among other things, says a bit about giving a talk.
Mark Leone’s page has a good collection of links to writing and miscellaneous academic resources.
Producing wrong data without doing anything obviously wrong! — Mytkowicz, Diwan, Hauswirth and Sweeney, ASPLOS 2009.
Derek Dreyer’s PLMW’16 talk “How to write papers so that people can read them” (slides here, video here).
Also helpful: Julia Evans’ Patterns in confusing explanations.
Ethan Perez, Easy Paper Writing Tips.
Zuckerman, Tips to article writers.
Étienne Fortier-Dubois, The elements of scientific style.
Boyle, now known as a founder of modern chemistry, argued in favour of making things interesting: A philosopher’s (or, as we would now say, a scientist’s) style ‘should delight its reader with his floridnesse’ and ‘disgust not its reader by its flatness’. A few years later, in a history of the Royal Society that is perhaps more accurately described as a manifesto, the clergyman and scientist Sprat disagreed, fighting fiercely against the use of tropes, metaphors, and ‘the volubility of tongue’.
Van Savage and Pamela Yeh: Cormac McCarthy’s tips on how to write a great science paper
- Use minimalism to achieve clarity. While you are writing, ask yourself: is it possible to preserve my original message without that punctuation mark, that word, that sentence, that paragraph or that section? Remove extra words or commas whenever you can.
- Decide on your paper’s theme and two or three points you want every reader to remember. This theme and these points form the single thread that runs through your piece. The words, sentences, paragraphs and sections are the needlework that holds it together. If something isn’t needed to help the reader to understand the main theme, omit it.
- Limit each paragraph to a single message. A single sentence can be a paragraph. Each paragraph should explore that message by first asking a question and then progressing to an idea, and sometimes to an answer. It’s also perfectly fine to raise questions in a paragraph and leave them unanswered.
Upon reflection, I’m ambivalent about this advice.
1.1 Mathematical
- Mathematical Writing, Donald E. Knuth, Tracy Larrabee and Paul M. Roberts. See particularly pages 31–35.
- Norman Ramsey’s notes for his class on Technical Writing.
- Mathematical Writing, by Donald E. Knuth et al. The first three sections make a minicourse on technical writing; it’s only eight pages. Reading it will repay us many times over.
- How to Write Mathematics, by P. R. Halmos.
- Igor Pak’s blog post, ‘How to Write Math Papers Clearly’, is also useful.
Jonathan Shewchuk, Three Sins of Authors in Computer Science and Math:
I’m not going to give you the usual advice that you fuss and fret over your introduction until it’s perfectly attuned to the psychological motivations of every potential reader. If everybody had time to do that, bad writing wouldn’t be a problem. Instead, I’m going to offer advice that will save you time: get to the point!
Nick Higham’s Handbook of Writing for the Mathematical Sciences has style and typographical tips that seem useful Not only may they make our writing easier to read, but they also act as identifiable signifiers of people who have read Higham, which is a useful shibboleth.
1.2 Machine learning papers
They’re a sub-sub-genre of their own.
2 Miscellaneous invective
Dan Robitzski: This Grad Student Used a Neural Network to Write His Papers (although the student credits the poor standards of the business school, not the amazing powers of GPT-2).
Roger’s Bacon: Research Papers Used to Have Style. What Happened?
E.T. Jaynes channelled through Tom Leinster on a generous reading of mathematics. We’ll need a good deal of patience to weather his verbose style.
If you differentiate a function \(f(x)\) without first having stated that it is differentiable, you are accused of lack of rigor. If you note that your function \(f(x)\) has some special property natural to the application, you are accused of lack of generality. In other words, every statement you make will receive the discourteous interpretation.…
fanatical insistence on one particular form of precision and generality can be carried so far that it defeats its own purpose; 20th century mathematics often degenerates into an idle adversary game instead of a communication process.
The fanatic is not trying to understand your substantive message at all, but only trying to find fault with your style of presentation. He will strive to read nonsense into what you are saying, if he can possibly find any way of doing so. In self-defense, writers are obliged to concentrate their attention on every tiny, irrelevant, nit-picking detail of how things are said rather than on what is said. The length grows; the content shrinks.
Mathematical communication would be much more efficient and pleasant if we adopted a different attitude. For one who makes the courteous interpretation of what others write, the fact that \(x\) is introduced as a variable already implies that there is some set \(X\) of possible values. Why should it be necessary to repeat that incantation every time a variable is introduced, thus using up two symbols where one would do? (Indeed, the range of values is usually indicated more clearly at the point where it matters, by adding conditions such as \((0 <x < 1)\) after an equation.)
For a courteous reader, the fact that a writer differentiates \(f(x)\) twice already implies that he considers it twice differentiable; why should he be required to say everything twice?
This offers a different diagnosis of a major ill than other competing complainants do. For example, Shaun Lehmann, the vagueness problem in academic writing:
[It is] likely that your writing was suffering from ‘vagueness’ — a constant problem in English. English-speaking readers (especially in an academic context) will only do a very small amount of work to figure out what you mean before they respond with confusion. […] A useful technique is to learn to read your work through the eyes of a kind of caricature of the low-context communication mode. You need to imagine a reader who is highly intelligent and logical, but who has no common sense and will fail to interpret any multiple meaning in the way you had intended.
I call my version of this the Commander Data Meditation […]
3 Process
4 Review and rebuttals
Cosma Shalizi, Practical peer review:
- The quality of peer review is generally abysmal.
- Peer reviewers are better readers of your work than almost anyone else.
Perhaps this will help: Learn to peer review with confidence
Gain practical experience in peer review with the Publons Academy, our free peer review training course. You’ll write real reviews with one-to-one guidance from your mentor, and gain exclusive access to our Review Template and examples. Upon graduation from the course, you’ll be a certified peer reviewer, ready to connect with top journal editors in your field.
Rob Hyndman’s Writing seminar It also provides bullet points on weathering reviews.
- Hints for Referees, Donald E. Knuth.
- A Guide for New Referees in Theoretical Computer Science, Ian Parberry.
- The Task of the Referee, Alan Jay Smith.
- How to Be an Outstanding Reviewer for the Journal of General Internal Medicine … and Other Journals, Carlos Estrada et al.