Differentiable model selection

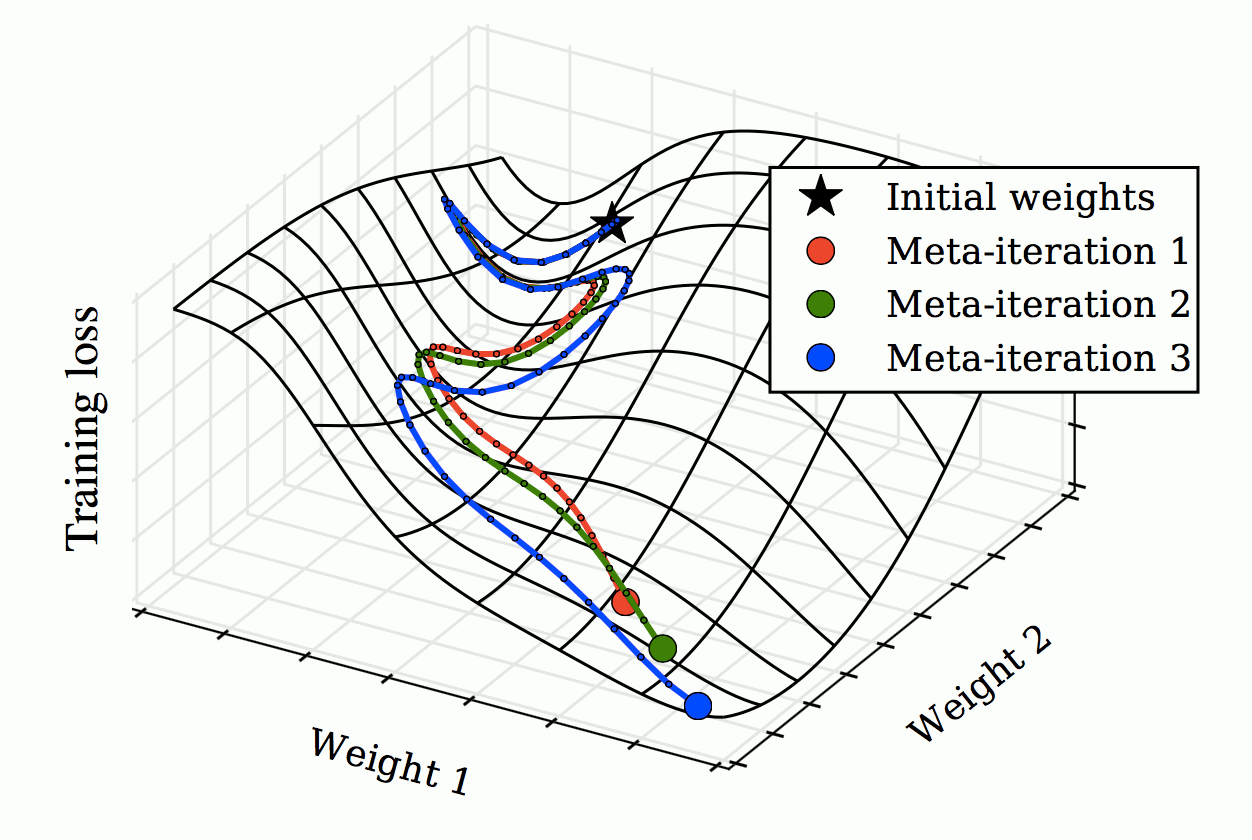
Each meta-iteration runs an entire training run of stochastic gradient descent to optimize elementary parameters (weights 1 and 2). Gradients of the validation loss with respect to hyperparameters are then computed by propagating gradients back through the elementary training iterations. Hyperparameters (in this case, learning rate and momentum schedules) are then updated in the direction of this hypergradient. … The last remaining parameter to SGD is the initial parameter vector. Treating this vector as a hyperparameter blurs the distinction between learning and meta-learning. In the extreme case where all elementary learning rates are set to zero, the training set ceases to matter and the meta-learning procedure exactly reduces to elementary learning on the validation set. Due to philosophical vertigo, we chose not to optimize the initial parameter vector.

Their implementation, hypergrad, is no longer maintained. Possibly the same, drmad by Fu et al. (2016), also not maintained.

This is a neat trick, but it has at least one clear limitation: it generally requires an estimate of the overfitting penalty as in the style of a degrees-of-freedom penalty. There are various assumptions on the optimisation and model process also that I forget right now, but they resemble the setting of learning odes and so are possibly worth examining through that lense.

Recent development

facebookresearch/higher: higher is a pytorch library allowing users to obtain higher order gradients over losses spanning training loops rather than individual training steps.

higher is a library providing support for higher-order optimization, e.g. through unrolled first-order optimization loops, of “meta” aspects of these loops. It provides tools for turning existing torch.nn.Module instances “stateless”, meaning that changes to the parameters thereof can be tracked, and gradient with regard to intermediate parameters can be taken. It also provides a suite of differentiable optimizers, to facilitate the implementation of various meta-learning approaches.

Full documentation is available at https://higher.readthedocs.io/en/latest/.