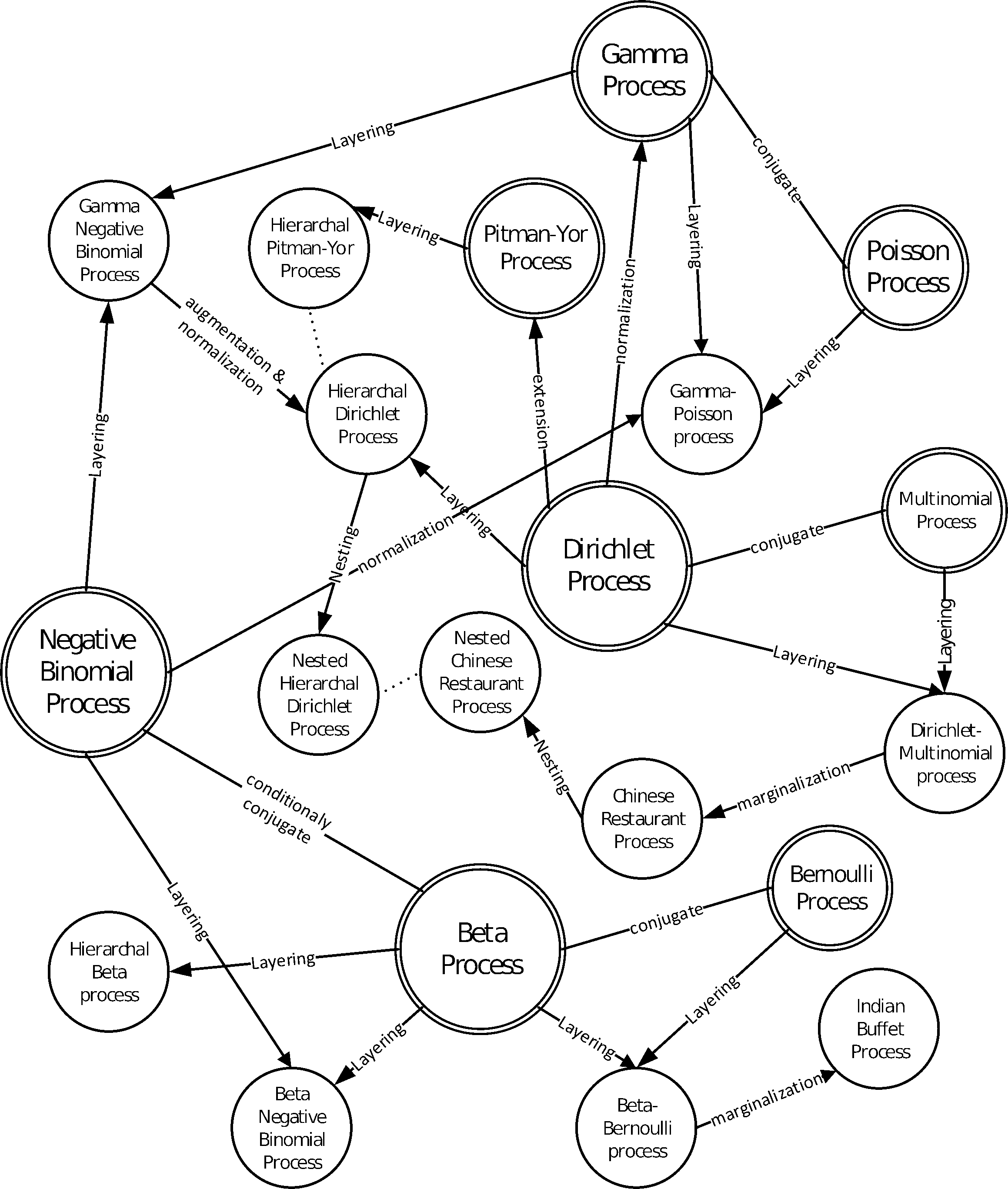
1 Useful stochastic processes
Dirichlet priors, other measure priors, Gaussian Process regression, reparameterisations etc. 🏗 There is a close connection to Bayes predictives.
2 Posterior updates in infinite dimensions
For now, this is just a bookmark to the general measure-theoretic notation that unifies, in principle, the various Bayesian nonparametric methods. A textbook on general theory is Schervish (2012). Chapter 1 of Matthews (2017) is a compact introduction.
Particular applications are outlined in Matthews (2017) (GP regression) and Stuart (2010) (inverse problems).
A brief introduction to the kind of measure-theoretic notation we need in the infinite-dimensional Hilbert space settings is in Alexanderian (2021), giving Bayes’ formula as
They observe
Note that in the finite-dimensional setting the abstract form of the Bayes’ formula above can be reduced to the familiar form of Bayes’ formula in terms of PDFs. Specifically, working in finite dimensions, with
and that are absolutely continuous with respect to the Lebesgue measure , the prior and posterior measures admit Lebesgue densities and , respectively. Then, we note
3 Bayesian consistency
Consistency turns out to be potentially tricky for functional models. I am not an expert on consistency, but see Cox (1993) for some warnings about what can go wrong and Florens and Simoni (2016);Knapik, van der Vaart, and van Zanten (2011) for some remedies. tl;dr posterior credible intervals arising from over-tight priors may never cover the frequentist estimate. Further reading on this is in some classic refs (Diaconis and Freedman 1986; Freedman 1999; Kleijn and van der Vaart 2006).