Gradient descent, Newton-like
2019-02-05 — 2024-01-15
Wherein second‑order curvature is examined and the role of Hessian approximations—Gauss‑Newton, generalized Gauss‑Newton and quasi‑Newton secant updates—are described as underpinning trust‑region and line‑search methods.
Suspiciously similar content
NB ⚠️⛔️☣️: Under reconstruction; I think I need to characterise the 2nd-order Hessian approximations better.
Newton-type optimization, unlike basic gradient descent, uses (possibly approximate) 2nd-order gradient information to find the argument which minimises
Optimization over arbitrary functions typically gets discussed in terms of line-search and trust-region methods, both of which can be construed, AFAICT, as second order methods. Although I don’t know of a first order trust region method; what would that even be? I think I don’t need to care about the distinction for the current purpose. We’ll see.
Can one do higher-than-2nd order optimisation? Of course. In practice, 2nd order is usually fast enough and has enough complications to keep one busy, so the greater complexity and per-iteration convergence rate of a 3rd order method does not usually offer an attractive trade-off.
Here are some scattered notes which make no claim to comprehensiveness, comprehensibility or coherence.
1 General
Robert Grosse, Second-Order Optimization is a beautiful introduction as part of CSC2541 Topics in Machine Learning: Neural Net Training Dynamics. There is a whole series (Grosse 2021a, 2021b, 2021c) of IMO beautifully written lectures on this.
2 One-dimensional Newton
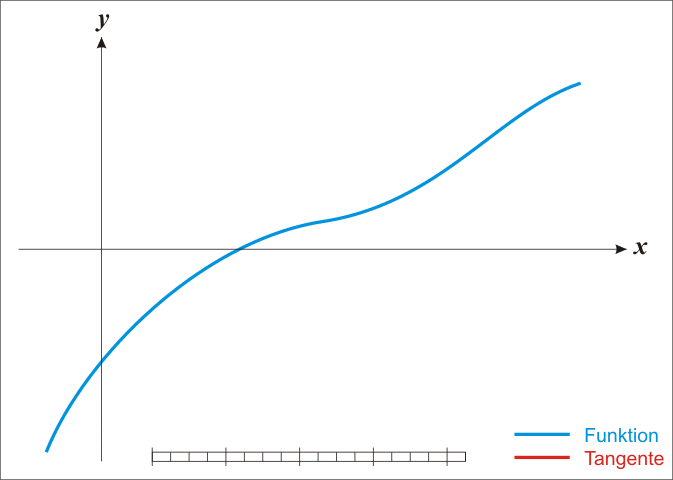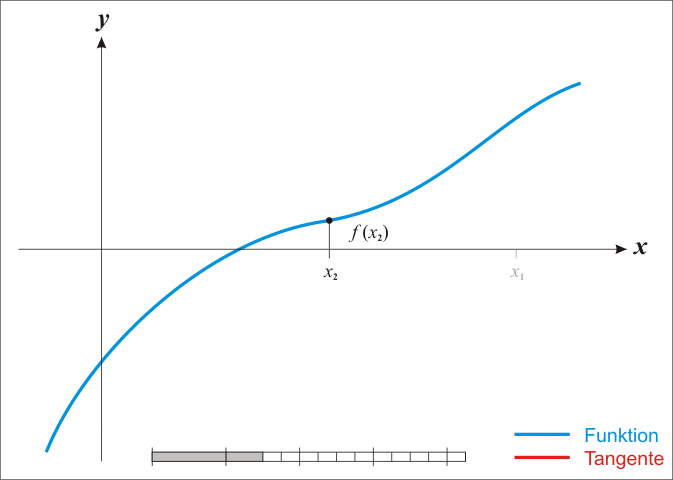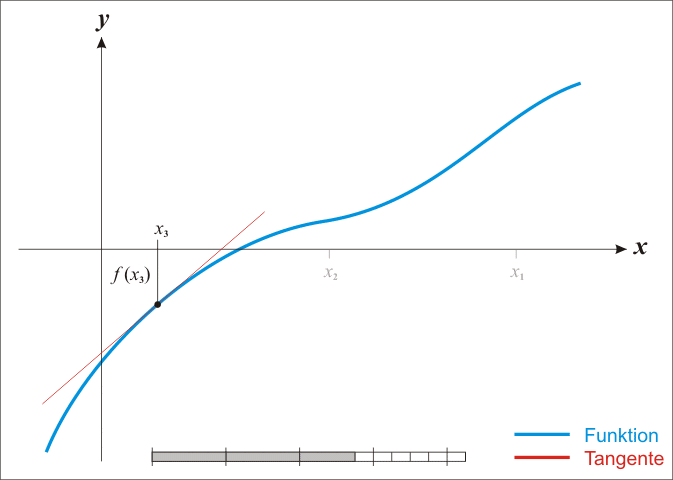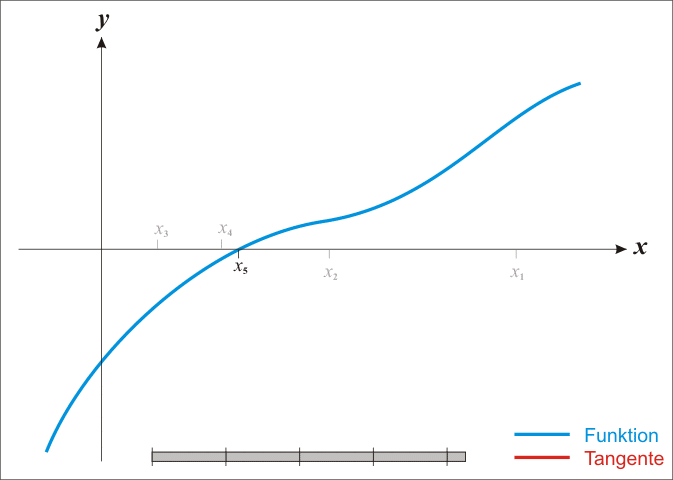
The basic case is simple; we get into difficulties with the multidimensional stuff in a moment. From school one might remember that classic so-called Newton method for iteratively improving a guessed location
Under the assumption that it is twice continuously differentiable, we can find stationary points—zeros of the derivative—of a function
How and why does this work again? Loosely, the argument is that we can use the Taylor expansion of a function to produce a locally quadratic model for the function, which might be not at all globally quadratic.
3 Multidimensional Newton
Returning to the objective with a multidimensional argument
Putting the remainder in Cauchy form, this tells us
Generally, we might take a local quadratic model for
If we ignore some subtleties and imagined this quadratic model was true, it would have an extremum where the directional derivative of this model vanished, i.e. $ m_x(p)$ where
From this we get the multidimensional Newton update rule, by choosing for each
In practice the quadratic model is not true (or we would be done in one step) and we would choose a more robust method that by using a trust region or line-search algorithm to handle the divergence between the model and its quadratic approximation. Either way the quadratic approximation would be used, which would mean that the inverse Hessian matrix
🏗 Unconstrained assumption, need for saddle points not just extrema with Lagrange methods, positive-definiteness etc.
4 Gauss-Newton
A reasonably clear Stackeschange answer that will do for now: Difference between Newton’s method and Gauss-Newton method.
5 Generalized Gauss-Newton
NB ⚠️⛔️☣️: This sections is vague half-arsed notes of dubious accuracy.
The generalized Gauss-Newton approximation (GGN) (Martens and Grosse 2015). replaces an expensive second order derivative by a product of first order derivatives. Used in (Foong et al. 2019; Immer, Korzepa, and Bauer 2021).
6 Fisher method
I haven’t actually worked out what this is yet, nor whether it relates or is filed correctly there. But I think that it is natural gradient descent.
7 Quasi Newton methods
Secant conditions and approximations to the Hessian. Let’s say we are designing a second-order update method. See e.g. Nocedal and Wright (2006).
In BFGS the approximate Hessian
Given the displacement
… We hope to get from this the secant condition.
TODO: compare and contrast to the Wolfe conditions on step length.
🏗
8 Hessian free
Second order optimisation that does not require the Hessian matrix to be given explicitly. I should work out the boundaries of this definition. Does it include Quasi Newton? CGD? Intersect with? Overlap? 🏗
Andre Gibiansky wrote an example for coders.
9 Stochastic
See stochastic 2nd order gradient descent for some bonus complications.