Numerical PDE solvers
March 1, 2016 — October 23, 2023
There are many methods for numerically solving partial differential equations. Finite element methods, geometric multigrid, algebraic multigrid. Stochastic methods… Building a solver from base principles is a wonderful and improving activity but something that I do not wish to do recreationally. For a list of particular methods designed to be differentiable in their parameters, see differentiable PDE solvers.
Here, I list some handy solvers that have crossed my radar for their use in research. Thus the list skews towards open-source. There are also commercial ones out there, but they are usually so expensive that a funding case must be made to acquire licenses and they have a meagre usage community; as such they are not favourable for my exploratory use.
1 HOWTO DIY
2 SOFA
Seems to be popular for soft materials simulations.
Today, SOFA gathers about 15 years of research in physics simulation. Many publications were accepted, several simulators were developed and five startups were created. The research topics were diverse:
- Solid mechanics with the simulation of the brain, the ear, the bones, the heart, the liver,
- Fluid dynamics with the simulation of fat filling and blood flow in aneurysms,
- Thermodynamics with thermo-ablation of tumors,
- and many other topics as image processing, animation or biological applications !
3 Clawpack
Clawpack is a collection of finite volume methods for linear and nonlinear hyperbolic systems of conservation laws. Clawpack employs high-resolution Godunov-type methods with limiters in a general framework applicable to many kinds of waves. Clawpack is written in Fortran and Python.
There is a python… interface? Port?
4 Dedelus
Dedalus solves differential equations using spectral methods. It’s open-source, written in Python, and MPI-parallelized.
We develop and use Dedalus to study fluid dynamics, but it’s designed to solve initial-value, boundary-value, and eigenvalue problems involving nearly arbitrary equations sets. You build a spectrally-representable domain, symbolically specify equations and boundary conditions, select a numerical solver, and go.
If my problem happens to be neatly expressible as a product of This one looks extra nice because sometimes I just want problems solved on a raster grid without all the flexibility of the FEM solvers.
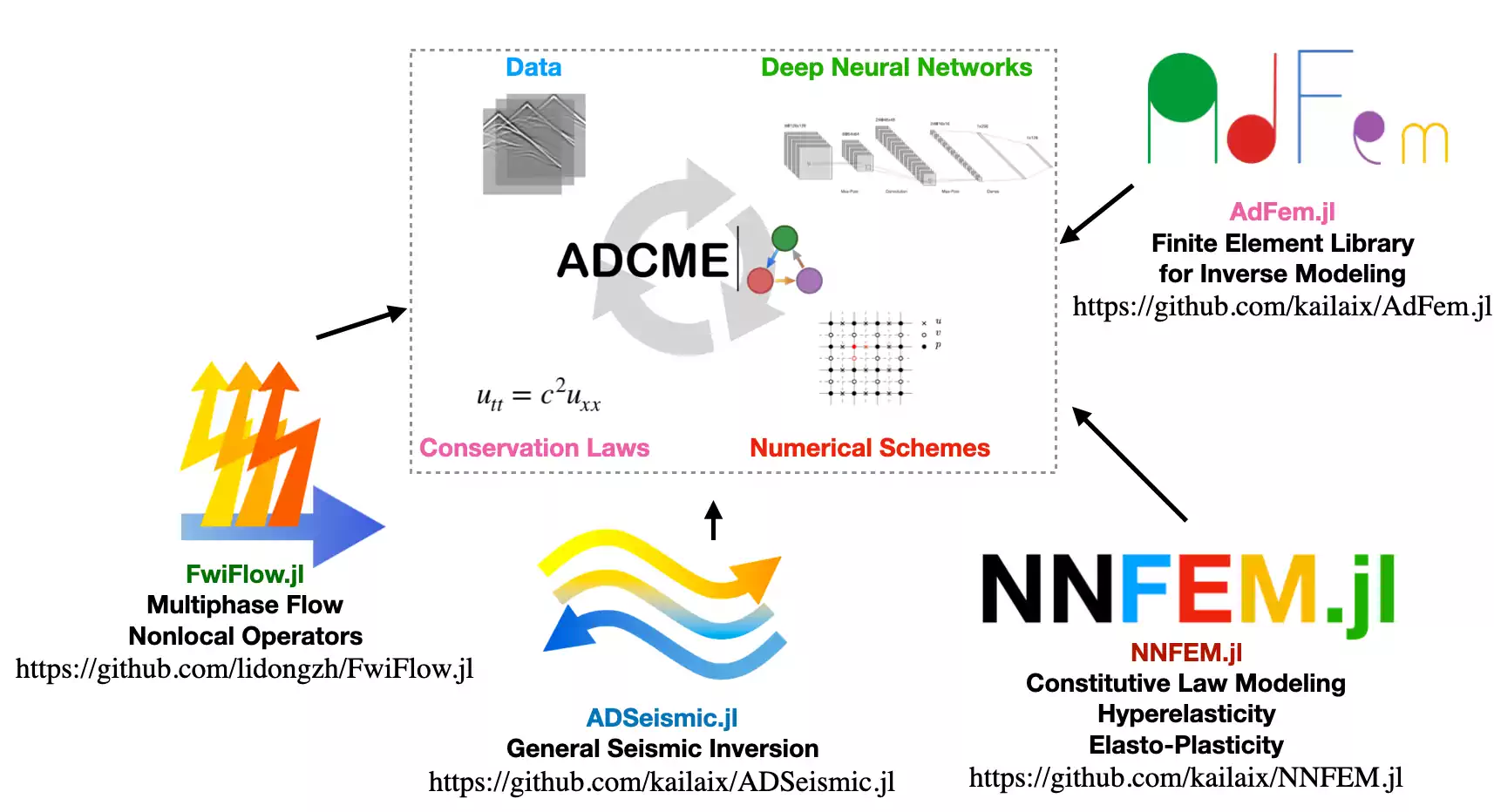
5 ADCME
A Julia system using Tensorflow to handle some of the autodiff mechanics.
ADCME is suitable for conducting inverse modeling in scientific computing; specifically, ADCME targets physics informed machine learning, which leverages machine learning techniques to solve challenging scientific computing problems. The purpose of the package is to:
- provide differentiable programming framework for scientific computing based on TensorFlow automatic differentiation (AD) backend;
- adapt syntax to facilitate implementing scientific computing, particularly for numerical PDE discretization schemes;
- supply missing functionalities in the backend (TensorFlow) that are important for engineering, such as sparse linear algebra, constrained optimization, etc.
Applications include
- physics informed machine learning (a.k.a., scientific machine learning, physics informed learning, etc.)
- coupled hydrological and full waveform inversion
- constitutive modeling in solid mechanics
- learning hidden geophysical dynamics
- parameter estimation in stochastic processes
The package inherits the scalability and efficiency from the well-optimized backend TensorFlow. Meanwhile, it provides access to incorporate existing C/C++ codes via the custom operators. For example, some functionalities for sparse matrices are implemented in this way and serve as extendable ”plugins” for ADCME.
AFAICT this implies that GPUs are not in general supported.
6 DIY in Julia
JuliaGeometry/Meshes.jl: Computational geometry and meshing algorithms in Julia
7 JuliaFEM
Julaifem is an umbrella organisation supporting julia-backed FEM solvers. The documentation is tricksy, but check out the examples. Analyses and solvers · JuliaFEM.jl
8 Trixi
Trixi.jl is a numerical simulation framework for hyperbolic conservation laws written in Julia. A key objective for the framework is to be useful to both scientists and students. Therefore, next to having an extensible design with a fast implementation, Trixi is focused on being easy to use for new or inexperienced users, including the installation and postprocessing procedures.
9 Gridap.jl
10 Firedrake
Firedrake seems popular for Python projects that do not need GPU?
Firedrake is an automated system for the solution of partial differential equations using the finite element method (FEM). Firedrake uses sophisticated code generation to provide mathematicians, scientists, and engineers with a very high productivity way to create sophisticated high performance simulations.
- Expressive specification of any PDE using the Unified Form Language from the FEniCS Project.
- Sophisticated, programmable solvers through seamless coupling with PETSc.…
- Sophisticated automatic optimisation, including sum factorisation for high order elements, and vectorisation.
11 FEniCS
Also seems to be a friendly PDE solver. Also lacking in GPU support (Alnæs et al. 2015, 2009, 2014; Alnæs, Logg, and Mardal 2012; Alnæs 2012; Kirby and Logg 2006; Kirby 2012; Logg, Mardal, et al. 2012; Logg and Wells 2010; Logg, Wells, and Hake 2012; Logg, Ølgaard, et al. 2012).
FEniCS is a popular open-source (LGPLv3) computing platform for solving partial differential equations (PDEs). FEniCS enables users to quickly translate scientific models into efficient finite element code. With the high-level Python and C++ interfaces to FEniCS, it is easy to get started, but FEniCS offers also powerful capabilities for more experienced programmers. .FEniCS runs on a multitude of platforms ranging from laptops to high-performance clusters.
As an illustration of how to program a simple PDE model with FEniCS, consider the Stokes equations in variational form:
\[\int_{\Omega} \mathrm{grad} \, u : \mathrm{grad} \, v \,\mathrm{d}x \, – \int_{\Omega} p \, \mathrm{div} \, v \,\mathrm{d}x + \int_{\Omega} \mathrm{div} \, u \, q \,\mathrm{d}x = \int_{\Omega} f \cdot v \,\mathrm{d}x.\]
The variational problem is easily transcribed into Python using mathematical operators in FEniCS:
# Define function space
P2 = VectorElement('P', tetrahedron, 2)
P1 = FiniteElement('P', tetrahedron, 1)
TH = P2 * P1
W = FunctionSpace(mesh, TH)
# Define variational problem
(u, p) = TrialFunctions(W)
(v, q) = TestFunctions(W)
a = inner(grad(u), grad(v))*dx - p*div(v)*dx + div(u)*q*dx
L = dot(f, v)*dx
# Compute solution
w = Function(W)
solve(a == L, w, [bc1, bc0])
12
13 scikit-fdidd
Nicolas Cellier / scikit-fdiff/Welcome to Scikit FiniteDiff’s documentation!
Scikit-fdiff is a python library that aim to solve partial derivative equations without pain. As its name says, it uses finite difference method to discretize the spatial derivative. As its name does not say, it is based on method of lines where all the dimension of the PDE but the last (the time) is discretized. That turns the PDE in a high-dimension ODE that can be solved with standard numerical integration of ODEs.
Annoyingly this does not seem to directly support adjoints, but it should not be too hard to hack.
14 PolyFEM
PolyFEM is a simple C++ and Python finite element library. We provide a wide set of common PDEs including:
- Laplace
- Helmholtz
- Linear Elasticity
- Saint-Venant Elasticity
- Neo-Hookean Elasticity
- Stokes
- Navier Stokes [beta]
PolyFEM simplicity lies on the interface: just pick a problem, select some boundary condition, and solve. No need to construct complicated function spaces, or learn a new scripting language: everything is set-up trough a JSON interface or through the Setting class in python.
15 SfePy
SfePy is a (sic) software for solving systems of coupled partial differential equations (PDEs) by the finite element method in 1D, 2D and 3D. It can be viewed both as black-box PDE solver, and as a Python package which can be used for building custom applications. The word “simple” means that complex FEM problems can be coded very easily and rapidly.
See Cimrman, Lukeš, and Rohan (2019).
16 fipy
fipy is original school:
FiPy is an object oriented, partial differential equation (PDE) solver, written in Python, based on a standard finite volume (FV) approach. … The FiPy framework includes terms for transient diffusion, convection and standard sources, enabling the solution of arbitrary combinations of coupled elliptic, hyperbolic and parabolic PDEs. Currently implemented models include phase field treatments of polycrystalline, dendritic, and electrochemical phase transformations as well as a level set treatment of the electrodeposition process.
usnistgov/fipy: FiPy is a Finite Volume PDE solver written in Python
17 PyAMG
pyamg is an algebraic multigrid solver, which is … a kind of multi-resolution method?
AMG is a multilevel technique for solving large-scale linear systems with optimal or near-optimal efficiency. Unlike geometric multigrid, AMG requires little or no geometric information about the underlying problem and develops a sequence of coarser grids directly from the input matrix. This feature is especially important for problems discretised on unstructured meshes and irregular grids:
A = poisson((500,500), format='csr') # 2D Poisson problem on 500x500 grid
ml = ruge_stuben_solver(A) # construct the multigrid hierarchy
print ml # print hierarchy information
b = rand(A.shape[0]) # pick a random right hand side
x = ml.solve(b, tol=1e-10) # solve Ax=b to a tolerance of 1e-8
print("residual norm is", norm(b - A*x)) # compute norm of residual vectorSee Yousef Saad’s textbooks on algebraic multigrid methods (free online).
18 Single-purpose solvers
nsfds2 is a Navier-Stokes solver in 2d especially for acoustics models