Differentiable PDE solvers
2017-05-15 — 2024-12-05
Wherein differentiable PDE solvers are presented as frameworks that expose discrete adjoint gradients for machine‑learning integration, and specific tools like PhiFlow and dolfin‑adjoint are cited.
Suppose we are keen to devise yet another method that will do clever things to augment PDE solvers with ML somehow. To that end, it would be nice to have a PDE solver that was not a completely black box but which we could interrogate for useful gradients to compare. Obviously, all PDE solvers use gradient information, but only some of them expose that to us as users as a first-class feature. For example, MODFLOW will give me a solution field but not the gradients of the field that were used to calculate that gradient. In ML toolkits, accessing this information is often easy; many of them supply an API to access adjoints.
On the other hand, there is a lot of sophisticated work done by PDE solvers that is hard for ML toolkits to recreate. That is why PDE solvers are a thing.
Classic PDE solvers which combine gradient-based (with respect to inputs) inference and ML outputs do exist. Differentiable solvers for PDEs combine a high fidelity to the supposed laws of physics governing the system under investigation with the potential to do some kind of inference through them. Obviously, they involve various approximations to the “ground truth” in practice; reality must be discretized and simplified to fit in the machine. However, the kinds of simplifications that these solvers make are by convention unthreatening; we generally are not too concerned about the discretisation implied by a finite-element method mesh, or the cells in a finite difference, or the waves in a spectral method, which we can often prove are “not too far” from what we would find in a physical system which truly followed the laws we hope it does. On the other hand, we might be suspicious that the laws of physics we do know are truly a complete characterisation of the system (pro tip: they are not) so these solvers might give us undue confidence that their idealized fidelity guarantees that they will be accurate to solve the real world, not mathematical idealisations of it. Further, these solvers often buy fidelity at the price of speed. Empirically, we discover that we can get nearly-as-good a result from an ML method but far faster than a classic PDE solver.
There is a role for both kinds of approaches; in fact, there is a burgeoning industry in stitching them together and playing off the relative strengths of each.
TBD: discuss how sufficiently flexible PDE solvers allow us to solve the adjoint equation and “manually” differentiate
Good. For now, some alternatives.
1 PhiFlow
PhiFlow: A differentiable PDE solving framework for machine learning (Holl et al. 2020).
I use this a lot, so it has its own notebook.
2 Exponax
3 jax-cfd
Unremarkable name, looks handy though. Implements both projection methods and spectral methods, and different variations of Crank-Nicholson for fluid-dynamical models. Seems to imply periodic boundary conditions?
4 DPFEHM
OrchardLANL/DPFEHM.jl: DPFEHM: A Differentiable Subsurface Flow Simulator
DPFEHM is a Julia module that includes differentiable numerical models with a focus on fluid flow and transport in the Earth’s subsurface. Currently, it supports the groundwater flow equations (single phase flow), Richards equation (air/water), the advection-dispersion equation, and the 2d wave equation.
Does not seem to support CUDA well but is nifty. Use in e.g. Pachalieva et al. (2022). Inverse solver example. NN example.
5 Trixi
Trixi.jl is a numerical simulation framework for hyperbolic conservation laws written in Julia. A key objective for the framework is to be useful to both scientists and students. Therefore, next to having an extensible design with a fast implementation, Trixi is focused on being easy to use for new or inexperienced users, including the installation and postprocessing procedures. Its features include:
- 1D, 2D, and 3D simulations on line/quad/hex/simplex meshes
- Cartesian and curvilinear meshes
- Conforming and non-conforming meshes
- Structured and unstructured meshes
- Hierarchical quadtree/octree grid with adaptive mesh refinement
- Forests of quadtrees/octrees with p4est via P4est.jl
- High-order accuracy in space in time
- Discontinuous Galerkin methods
- Kinetic energy-preserving and entropy-stable methods based on flux differencing
- Entropy-stable shock capturing
- Positivity-preserving limiting
- Finite difference summation by parts (SBP) methods
- Compatible with the SciML ecosystem for ordinary differential equations
- Explicit low-storage Runge-Kutta time integration
- Strong stability preserving methods
- CFL-based and error-based time step control
- Native support for differentiable programming
- Forward mode automatic differentiation via ForwardDiff.jl
- Periodic and weakly-enforced boundary conditions
6 torchphysics
TorchPhysics is a Python library of (mesh-free) deep learning methods to solve differential equations. You can use TorchPhysics e.g. to
- solve ordinary and partial differential equations
- train a neural network to approximate solutions for different parameters
- solve inverse problems and interpolate external data
Much NN automation in this library but the NN part is bare-bones FEM stuff.
7 Tornadox
Using Bayesian probabilistic numerics? TBD. See tornadox (Krämer et al. 2021).
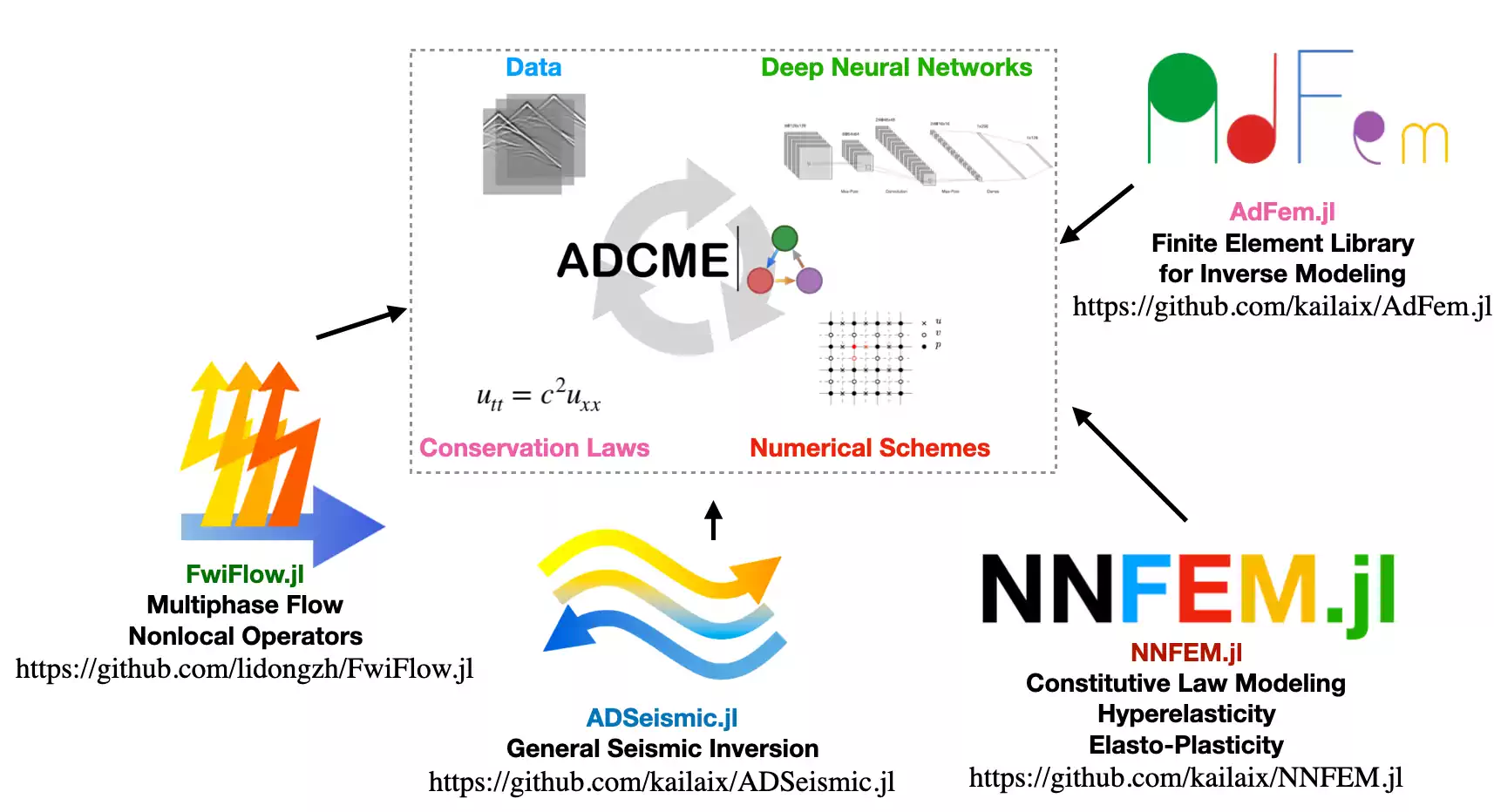
8 ADCME
ADCME is suitable for conducting inverse modeling in scientific computing; specifically, ADCME targets physics informed machine learning, which leverages machine learning techniques to solve challenging scientific computing problems. The purpose of the package is to:
- provide differentiable programming framework for scientific computing based on TensorFlow automatic differentiation (AD) backend;
- adapt syntax to facilitate implementing scientific computing, particularly for numerical PDE discretization schemes;
- supply missing functionalities in the backend (TensorFlow) that are important for engineering, such as sparse linear algebra, constrained optimization, etc.
Applications include
- physics informed machine learning (a.k.a., scientific machine learning, physics informed learning, etc.)
- coupled hydrological and full waveform inversion
- constitutive modeling in solid mechanics
- learning hidden geophysical dynamics
- parameter estimation in stochastic processes
The package inherits the scalability and efficiency from the well-optimized backend TensorFlow. Meanwhile, it provides access to incorporate existing C/C++ codes via the custom operators. For example, some functionalities for sparse matrices are implemented in this way and serve as extendable “plugins” for ADCME.
9 OpenFOAM
OpenFOAM (for “Open-source Field Operation And Manipulation”) is a C++ toolbox for the development of customized numerical solvers, and pre-/post-processing utilities for the solution of continuum mechanics problems, most prominently including computational fluid dynamics (CFD).
The adjoint optimisation takes some digging to discover. Keyword: adjointOptimisationFoam (E. Papoutsis-Kiachagias et al. 2021).
10 JuliaFEM
JuliaFEM is an umbrella organisation supporting Julia-backed FEM solvers. The documentation is tricksy, but check out the examples, Supported solvers listed here. I assume these are all differentiable, since that is a selling point of the SciML.jl ecosystem they spring from, but I have not checked. The emphasis seems to be upon cluster-distributed solutions at scale.
11 FEniCS
Also seems to be a friendly PDE solver, lacking in GPU support. However, it does have an interface to pytorch, barkm/torch-fenics on the CPU to provide differentiability with respect to parameters.
12 dolfin-adjoint
dolfin-adjoint (Mitusch, Funke, and Dokken 2019):
The dolfin-adjoint project automatically derives the discrete adjoint and tangent linear models from a forward model written in the Python interface to FEniCS and Firedrake
These adjoint and tangent linear models are key ingredients in many important algorithms, such as data assimilation, optimal control, sensitivity analysis, design optimisation, and error estimation. Such models have made an enormous impact in fields such as meteorology and oceanography, but their use in other scientific fields has been hampered by the great practical difficulty of their derivation and implementation. In his recent book Naumann (2011) states that
[T]he automatic generation of optimal (in terms of robustness and efficiency) adjoint versions of large-scale simulation code is one of the great open challenges in the field of High-Performance Scientific Computing.
The dolfin-adjoint project aims to solve this problem for the case where the model is implemented in the Python interface to FEniCS/Firedrake.
This provides the AD backend to barkm/torch-fenics which integrates with pytorch.
13 Engys Helyx
HELYX is a unified, off-the-shelf CFD software product compatible with most Linux and Windows platforms, including high-performance computing systems. In addition to the base software components delivered for installation (HELYX-GUI and HELYX-Core), the package also incorporates an extensive set of ancillary services to facilitate the deployment and usage of the software in any working environment.
HELYX features an advanced hex-dominant automatic mesh algorithm with polyhedra support which can run in parallel to generate large computational grids. The solver technology is based on the standard finite-volume approach, covering a wide range of physical models: single- and multi-phase turbulent flows (RANS, URANS, DES, LES), thermal flows with natural/forced convection, thermal/solar radiation, incompressible and compressible flow solutions, etc. In addition to these, we have developed a Generalised Internal Boundaries (GIB) method to support complex boundary motions inside the finite-volume mesh. The standard capabilities of HELYX can also be expanded with the HELYX-ADD-ONS extension modules to cover more specialised applications.
HELYX-Adjoint is a continuous adjoint CFD solver for topology and shape optimisation developed by ENGYS based on the extensive theoretical work of Dr. Carsten Othmer of Volkswagen AG, Corporate Research. The technology has been extensively proven and validated through productive use in real-life design applications, including: vehicle external aerodynamics, in-cylinder flows, HVAC ducts, turbomachinery components, battery cooling channels, among others.
14 Mantaflow
mantaflow - an extensible framework for fluid simulation:
mantaflow is an open-source framework targeted at fluid simulation research in Computer Graphics and Machine Learning. Its parallelized C++ solver core, python scene definition interface and plugin system allow for quickly prototyping and testing new algorithms. A wide range of Navier-Stokes solver variants are included. It’s very versatile, and allows coupling and import/export with deep learning frameworks (e.g., tensorflow via numpy) or standalone compilation as matlab plugin. Mantaflow also serves as the simulation engine in Blender.
Feature list:
The framework can be used with or without GUI on Linux, MacOS and Windows. Here is an incomplete list of features implemented so far:
- Eulerian simulation using MAC Grids, PCG pressure solver and MacCormack advection
- Flexible particle systems
- FLIP simulations for liquids
- Surface mesh tracking
- Free surface simulations with levelsets, fast marching
- Wavelet and surface turbulence
- K-epsilon turbulence modeling and synthesis
- Maya and Blender export for rendering
Mantaflow’s particular selling point is producing stunning 3d animations as an output. It is not widely used for inference in practice; people, including the authors, seem to prefer Phiflow for that end.
15 DeepXDE
DeepXDE is the reference solver implementation for PINN and DeepONet. (Lu et al. 2021)
Use DeepXDE if you need a deep learning library that
- solves forward and inverse partial differential equations (PDEs) via physics-informed neural network (PINN),
- solves forward and inverse integro-differential equations (IDEs) via PINN,
- solves forward and inverse fractional partial differential equations (fPDEs) via fractional PINN (fPINN),
- approximates functions from multi-fidelity data via multi-fidelity NN (MFNN),
- approximates nonlinear operators via deep operator network (DeepONet),
- approximates functions from a dataset with/without constraints.
You might need to moderate your expectations a little. I did, after that bold description. This is an impressive library, but as covered above, some of the types of problems it can solve are more limited than one might hope upon reading the description. Think of it as a neural network library that handles certain PDE calculations and you will not go too far astray.
16 TenFEM
TenFEM offers a small selection of differentiable FEM solvers for Tensorflow.
17 taichi
“Sparse simulator” Tai Chi (Hu et al. 2019) is presumably also able to solve PDEs? 🤷🏼♂️ If so that would be nifty because it is also differentiable. I suspect it is more of a graph network approach.