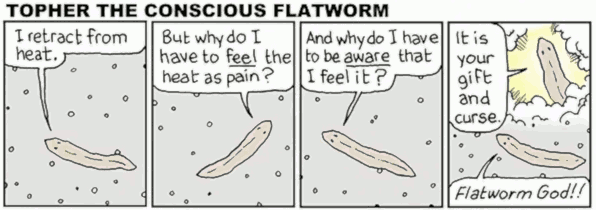
Bounded rationality
Plus miscellaneous rationality postulates restricting von Neumann-Morgenstern
January 13, 2012 — January 15, 2022
Prospect theory, Kahneman-and-Tversky style. Rational Heuristics, Gigerenzer-and-Todd style. Docility, Herbert-Simon-wise. Behavioural economics more generally.
- Such research is the bread-and-butter of PR and advertising agencies, PsyOps departments and interior designers the world over, but they don’t usually publish.
- The way the brain buys is a summary of “neuromarketing” in The Economist
- Finite Rationality and Interpersonal Complexity in Repeated Games, E. Kalai & W. Stanford
1 In markets and societies
2 For risk
See risk perception.
3 For learning and action
Can we get anywhere with predictive coding?
4 …and trust
Maybe trust machines.
5 In groups
Let us think of the wisdom of crowds.
6 Introspective
7 Incoming
Thinking about this very computationally is the mainstay of APXHARD, e.g. P ⊂ NP causes Political Polarization
DRMacIver’s Notebook: Three key problems with Von-Neumann Morgenstern Utility Theory
The first part is about physical difficulties with measurement—you can only know the probabilities up to some finite precision. VNM theory handwaves this away by saying that the probabilities are perfectly known, but this doesn’t help you because that just moves the problem to be a computational one, and requires you to be able to solve the halting problem. e.g. choose between \(L_1=p B+(1-p) W\) and \(L_2=q B+(1-q) W\) where \(p=0.0 \ldots\) until machine \(M 1\) halts and 1 after and \(q\) is the same but for machine \(M 2\).
The second demonstrates that what you get out of the VNM theorem is not a utility function. It is an algorithm that produces a sequence converging to a utility function, and you cannot recreate even the original decision procedure from that sequence without being able to take the limit (which requires running an infinite computation, again giving you the ability to solve the halting problem) near the boundary.