Data summarization
a.k.a Data distillation. sketching
2019-01-14 — 2025-02-23
Suspiciously similar content
Summary statistics don’t require us to keep the data but allow us to do inference nearly as well. For example, sufficient statistics in exponential families let us perform broad kinds of inference perfectly with just summaries, the smallest of which we call minimal sufficient statistics. Most statistical problems are more complex, though, and the technically minimal statistics of the dataset for those problems is the dataset itself. The question arises: can we do inference nearly as well as with the full dataset, but with a much smaller summary?
Methods like variational Bayes summarise the posterior likelihood by maintaining an approximating posterior density that encodes the information in the data likelihood at some cost in accuracy. Sometimes, the best summary of the posterior likelihood is not a density directly, but something like a smaller version of the dataset itself.
Outside of the Bayesian setting, we might not want to think about a posterior density but rather some predictive performance. I understand that this works as well, but I know less about the details.
There are many variants of this idea:
- Thinning, which is a term I learned from Carrell et al. (2025)
- Inducing sets, as seen in Gaussian processes
- Coresets
- Bounded Memory Learning considers using only some data from a computational complexity standpoint — is that related?
- Some dimension reductions are data summarisation but in a different sense than in this notebook; the summaries no longer look like the data.
- Many of the Foundation models end up being very efficiently trainable on well-chosen subsets of the data.
- In algorithm design, we summarise the data for a specific algorithm purpose rather than general inference. This is called sketching.
Different but related:
- More generally, we might try to collect optimal data adaptively
- Or even synthesise data that is representative of the original data with respect to our learning algorithm.
1 Bayes duality
“The new learning paradigm will be based on a new principle of machine learning, which we call the Bayes-Duality principle and will develop during this project. Conceptually, the new principle hinges on the fundamental idea that an AI should be capable of efficiently preserving and acquiring the relevant past knowledge, for a quick adaptation in the future. We will apply the principle to representation of the past knowledge, faithful transfer to new situations, and collection of new knowledge whenever necessary.”
Connection to Bayes by Backprop, continual learning, and neural memory?
2 Coresets
Solve an optimisation problem to minimise the distance between the posterior with all data, and with a weighted subset.
For example, trevorcampbell/bayesian-coresets.
3 Representative subsets
I think this is intended to be generic, i.e. not necessarily Bayesian. See apricot:
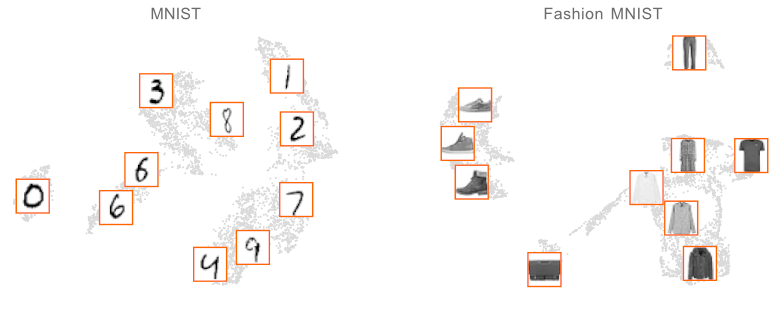
“Apricot implements submodular optimisation for the purpose of summarising massive datasets into minimally redundant subsets that are still representative of the original data. These subsets are useful for visualising the modalities in the data (such as in the two datasets below) and for training accurate machine learning models with just a fraction of the examples and compute.”
4 By influence functions
Include data based on how much it changes the predictions. Classic approach (Cook 1977; Thomas and Cook 1990) for linear models. Can also be applied to DL models, apparently. A bayes-by-backprop approach is Nickl et al. (2023) and a heroic second-order method is Grosse et al. (2023).
5 Sketching
See e.g. Cormode (2023):
Data summaries (a.k.a., sketches) are compact data structures that can be updated flexibly and efficiently to capture certain properties of a dataset. Well-known examples include set summaries (Bloom Filters) and cardinality estimators (e.g., Hyperloglog), amongst others. PODS and SIGMOD have been home to many papers on sketching, including several best paper recipients. Sketch algorithms have emerged from the theoretical research community but have found wide impact in practice. This paper describes some of the impacts that sketches have had, from online advertising to privacy-preserving data analysis. It will consider the range of different strategies that researchers can follow to encourage the adoption of their work, and what has and has not worked for sketches as a case study.
6 Data attribution
Generalised influence functions.