Markov Chain Monte Carlo methods

2017-08-28 – 2019-10-18

Despite studying within this area, I have nothing to say about MCMC broadly, but I do have some things I wish to keep notes on.

Hamiltonian Monte Carlo

An MCMC method induce by physics.

Connection to variational inference

Nifty. See (Salimans, Kingma, and Welling 2015)

Adaptive MCMC

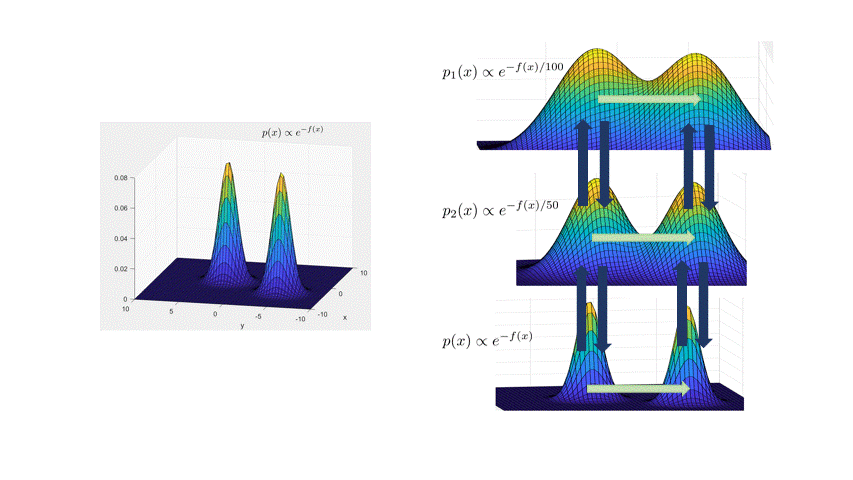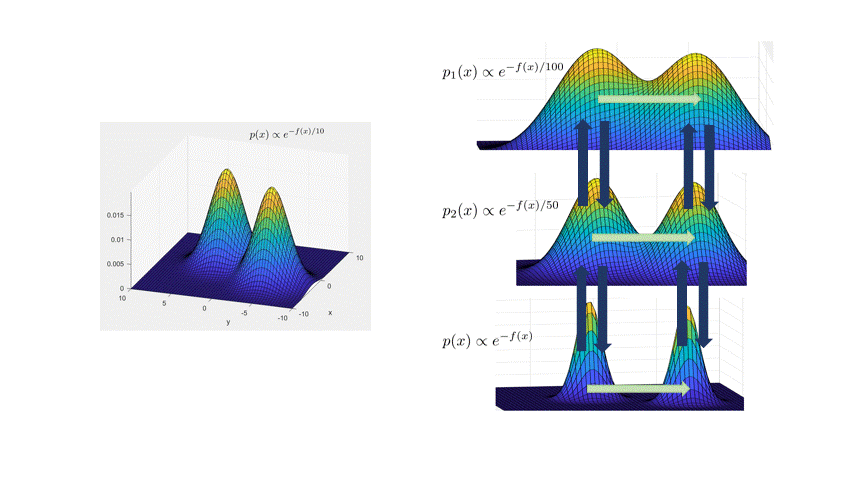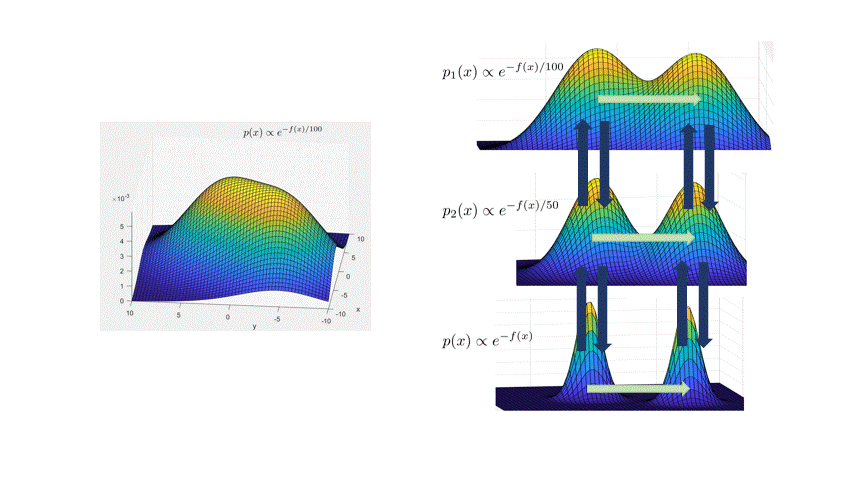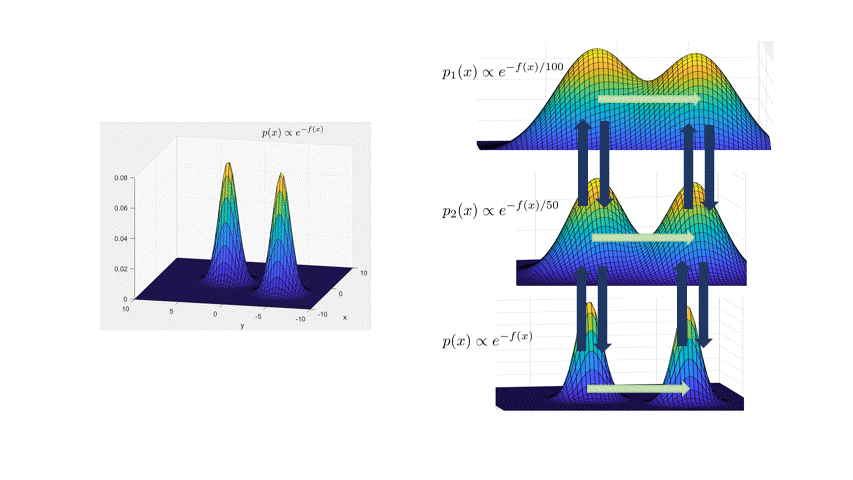
a.k.a. controlled MCMC. Here we are no longer truly using a Markov chain because the transitions parameters depend upon the entire history of the chain (for example because you are dynamically updating the mixing parameters). Tutorials: (Atchadé et al. 2011; Andrieu and Thoms 2008) To investigate: How (Schuster et al. 2015) work around this via a kernel trick.

Handy tricks

Pierre E. Jacob, John O’Leary, Yves Atchadé made MCMC estimators without finite-time-bias, which is nice for parallelisation. (Jacob, O’Leary, and Atchadé 2017)

Andrieu, Christophe, and Johannes Thoms. 2008. “A Tutorial on Adaptive MCMC.” Statistics and Computing 18 (4): 343–73. https://doi.org/10.1007/s11222-008-9110-y.

Atchadé, Yves, Gersende Fort, Eric Moulines, and Pierre Priouret. 2011. “Adaptive Markov Chain Monte Carlo: Theory and Methods.” In Bayesian Time Series Models, edited by David Barber, A. Taylan Cemgil, and Silvia Chiappa, 32–51. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9780511984679.003.

Bach, Francis. 2015. “On the Equivalence Between Kernel Quadrature Rules and Random Feature Expansions.” arXiv Preprint arXiv:1502.06800. http://arxiv.org/abs/1502.06800.

Bales, Ben, Arya Pourzanjani, Aki Vehtari, and Linda Petzold. 2019. “Selecting the Metric in Hamiltonian Monte Carlo,” May. http://arxiv.org/abs/1905.11916.

Betancourt, Michael. 2017. “A Conceptual Introduction to Hamiltonian Monte Carlo,” January. http://arxiv.org/abs/1701.02434.

———. 2018. “The Convergence of Markov Chain Monte Carlo Methods: From the Metropolis Method to Hamiltonian Monte Carlo.” Annalen Der Physik, March. https://doi.org/10.1002/andp.201700214.

Betancourt, Michael, Simon Byrne, Sam Livingstone, and Mark Girolami. 2017. “The Geometric Foundations of Hamiltonian Monte Carlo.” Bernoulli 23 (4A): 2257–98. https://doi.org/10.3150/16-BEJ810.

Calderhead, Ben. 2014. “A General Construction for Parallelizing Metropolis−Hastings Algorithms.” Proceedings of the National Academy of Sciences 111 (49): 17408–13. https://doi.org/10.1073/pnas.1408184111.

Carpenter, Bob, Matthew D. Hoffman, Marcus Brubaker, Daniel Lee, Peter Li, and Michael Betancourt. 2015. “The Stan Math Library: Reverse-Mode Automatic Differentiation in C++.” arXiv Preprint arXiv:1509.07164. http://arxiv.org/abs/1509.07164.

Cornish, Robert, Paul Vanetti, Alexandre Bouchard-Côté, George Deligiannidis, and Arnaud Doucet. 2019. “Scalable Metropolis-Hastings for Exact Bayesian Inference with Large Datasets,” January. http://arxiv.org/abs/1901.09881.

Diaconis, Persi, and David Freedman. 1999. “Iterated Random Functions.” SIAM Review 1 (1): 45–76. https://doi.org/10.1137/S0036144598338446.

Durmus, Alain, and Eric Moulines. 2016. “High-Dimensional Bayesian Inference via the Unadjusted Langevin Algorithm,” May. http://arxiv.org/abs/1605.01559.

Girolami, Mark, and Ben Calderhead. 2011. “Riemann Manifold Langevin and Hamiltonian Monte Carlo Methods.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 73 (2): 123–214. https://doi.org/10.1111/j.1467-9868.2010.00765.x.

Goodman, Noah, Vikash Mansinghka, Daniel Roy, Keith Bonawitz, and Daniel Tarlow. 2012. “Church: A Language for Generative Models,” June. http://arxiv.org/abs/1206.3255.

Goodrich, Ben, Andrew Gelman, Matthew D. Hoffman, Daniel Lee, Bob Carpenter, Michael Betancourt, Marcus Brubaker, Jiqiang Guo, Peter Li, and Allen Riddell. 2017. “Stan : A Probabilistic Programming Language.” Journal of Statistical Software 76 (1). https://doi.org/10.18637/jss.v076.i01.

Hodgkinson, Liam, Robert Salomone, and Fred Roosta. 2019. “Implicit Langevin Algorithms for Sampling from Log-Concave Densities,” March. http://arxiv.org/abs/1903.12322.

Jacob, Pierre E., John O’Leary, and Yves F. Atchadé. 2017. “Unbiased Markov Chain Monte Carlo with Couplings,” August. http://arxiv.org/abs/1708.03625.

Korattikara, Anoop, Yutian Chen, and Max Welling. 2015. “Sequential Tests for Large-Scale Learning.” Neural Computation 28 (1): 45–70. https://doi.org/10.1162/NECO_a_00796.

Lele, S. R., B. Dennis, and F. Lutscher. 2007. “Data Cloning: Easy Maximum Likelihood Estimation for Complex Ecological Models Using Bayesian Markov Chain Monte Carlo Methods.” Ecology Letters 10 (7): 551. https://doi.org/10.1111/j.1461-0248.2007.01047.x.

Lele, Subhash R., Khurram Nadeem, and Byron Schmuland. 2010. “Estimability and Likelihood Inference for Generalized Linear Mixed Models Using Data Cloning.” Journal of the American Statistical Association 105 (492): 1617–25. https://doi.org/10.1198/jasa.2010.tm09757.

Liu, Jun S. 1996. “Metropolized Independent Sampling with Comparisons to Rejection Sampling and Importance Sampling.” Statistics and Computing 6 (2): 113–19. https://doi.org/10.1007/BF00162521.

Mangoubi, Oren, and Aaron Smith. 2017. “Rapid Mixing of Hamiltonian Monte Carlo on Strongly Log-Concave Distributions,” August. http://arxiv.org/abs/1708.07114.

Neal, Radford M. 1993. “Probabilistic Inference Using Markov Chain Monte Carlo Methods.” Technical Report CRGTR-93-1. Toronto Canada: Department of Computer Science, University of Toronto, https://www.cs.princeton.edu/courses/archive/fall07/cos597C/readings/Neal1993.pdf.

———. 2011. “MCMC Using Hamiltonian Dynamics.” In Handbook for Markov Chain Monte Carlo, edited by Steve Brooks, Andrew Gelman, Galin L. Jones, and Xiao-Li Meng. Boca Raton: Taylor & Francis. http://arxiv.org/abs/1206.1901.

———. 2004. “Improving Asymptotic Variance of MCMC Estimators: Non-Reversible Chains Are Better,” July. http://arxiv.org/abs/math/0407281.

Norton, Richard A., and Colin Fox. 2016. “Tuning of MCMC with Langevin, Hamiltonian, and Other Stochastic Autoregressive Proposals,” October. http://arxiv.org/abs/1610.00781.

Propp, James Gary, and David Bruce Wilson. 1996. “Exact Sampling with Coupled Markov Chains and Applications to Statistical Mechanics.” In Random Structures & Algorithms, 9:223–52. New York, NY, USA: John Wiley & Sons, Inc. https://doi.org/10.1002/(SICI)1098-2418(199608/09)9:1/2<223::AID-RSA14>3.0.CO;2-O.

———. 1998. “Coupling from the Past: A User’s Guide.” In Microsurveys in Discrete Probability, edited by David Aldous and James Gary Propp, 41:181–92. DIMACS Series in Discrete Mathematics and Theoretical Computer Science. Providence, Rhode Island: American Mathematical Society. https://doi.org/10.1090/dimacs/041.

Rubinstein, Reuven Y, and Dirk P Kroese. 2004. The Cross-Entropy Method a Unified Approach to Combinatorial Optimization, Monte-Carlo Simulation and Machine Learning. New York, NY: Springer New York. http://dx.doi.org/10.1007/978-1-4757-4321-0.

Rubinstein, Reuven Y., and Dirk P. Kroese. 2016. Simulation and the Monte Carlo Method. 3 edition. Wiley Series in Probability and Statistics. Hoboken, New Jersey: Wiley.

Rubinstein, Reuven Y., Ad Ridder, and Radislav Vaisman. 2014. Fast Sequential Monte Carlo Methods for Counting and Optimization. Wiley Series in Probability and Statistics. Hoboken, New Jersey: Wiley.

Salimans, Tim, Diederik Kingma, and Max Welling. 2015. “Markov Chain Monte Carlo and Variational Inference: Bridging the Gap.” In Proceedings of the 32nd International Conference on Machine Learning (ICML-15), 1218–26. ICML’15. Lille, France: JMLR.org. http://proceedings.mlr.press/v37/salimans15.html.

Schuster, Ingmar, Heiko Strathmann, Brooks Paige, and Dino Sejdinovic. 2015. “Kernel Sequential Monte Carlo,” October. http://arxiv.org/abs/1510.03105.

Sisson, S. A., Y. Fan, and Mark M. Tanaka. 2007. “Sequential Monte Carlo Without Likelihoods.” Proceedings of the National Academy of Sciences 104 (6): 1760–5. https://doi.org/10.1073/pnas.0607208104.

Xifara, T., C. Sherlock, S. Livingstone, S. Byrne, and M. Girolami. 2014. “Langevin Diffusions and the Metropolis-Adjusted Langevin Algorithm.” Statistics & Probability Letters 91 (Supplement C): 14–19. https://doi.org/10.1016/j.spl.2014.04.002.

Xu, Kai, Hong Ge, Will Tebbutt, Mohamed Tarek, Martin Trapp, and Zoubin Ghahramani. 2019. “AdvancedHMC.Jl: A Robust, Modular and Efficient Implementation of Advanced HMC Algorithms,” October. https://openreview.net/forum?id=rJgzckn4tH.

Yoshida, Ryo, and Mike West. 2010. “Bayesian Learning in Sparse Graphical Factor Models via Variational Mean-Field Annealing.” Journal of Machine Learning Research 11 (May): 1771–98. http://www.jmlr.org/papers/v11/yoshida10a.html.