Neurons
Neural networks made of real neurons, in functioning brains
2014-11-03 — 2022-02-14
Wherein neural computation is presented at an intermediate scale and is described as being driven by discrete spikes in continuous time, with heterogeneous cell types and messy organisation being noted.
How do brains work?
I mean, how do brains work at a level slightly higher than a synapse, but much lower than, e.g. psychology. “How is thought done?” etc.
Notes pertaining to large, artificial networks are filed under artificial neural networks. The messy, biological end of the stick is here. Since brains seem to be the seat of the most flashy and important bit of the computing taking place in our bodies, we understandably want to know how they work, in order to
- fix Alzheimer’s disease
- steal cool learning tricks
- endow the children of elites with superhuman mental prowess to cement their places as Übermenschen fit to rule the thousand-year Reich
- …or whatever.
Real brains are different from the “neuron-inspired” computation of the simulacrum in many ways, not just the usual difference between model and reality. The similitude between “neural networks” and neurons is intentionally weak for reasons of convenience.
For one example, most simulated neural networks are based on a continuous activation potential and discrete time, unlike spiking biological ones which are driven by discrete events in continuous time.
Also, real brains support heterogeneous types of neurons, have messier layer organisation, use less power, don’t have well-defined backpropagation (or not in the same way), and many other things that I as a non-specialist do not know.
To learn more about:
- Just saw a talk by Dan Cireșan in which he mentioned the importance of “Foveation” — blurring the edge of an image when training classifiers on it, thus encouraging us to ignore stuff in order to learn better. What is, rigorously speaking, happening there? Nice actual crossover between biological neural nets and fake ones.
- Algorithmic statistics of neurons sounds interesting.
- Modelling mind as machine learning.
1 Fun data
2 How computationally complex is a neuron?
Empirically quantifying computation is hard, but people try to do it all the time for brains. Classics try to estimate structure in neural spike trains, (Crumiller et al. 2011; Haslinger, Klinkner, and Shalizi 2010; Nemenman, Bialek, and de Ruyter van Steveninck 2004) often by empirical entropy estimates.
If we are prepared to accept “size of a neural network needed to approximate X” as an estimate of the complexity of X, then there are some interesting results: Allison Whitten, How Computationally Complex Is a Single Neuron? (Beniaguev, Segev, and London 2021). OTOH, finding the smallest neural network that can approximate something is itself computationally hard and not in general even easy to check.
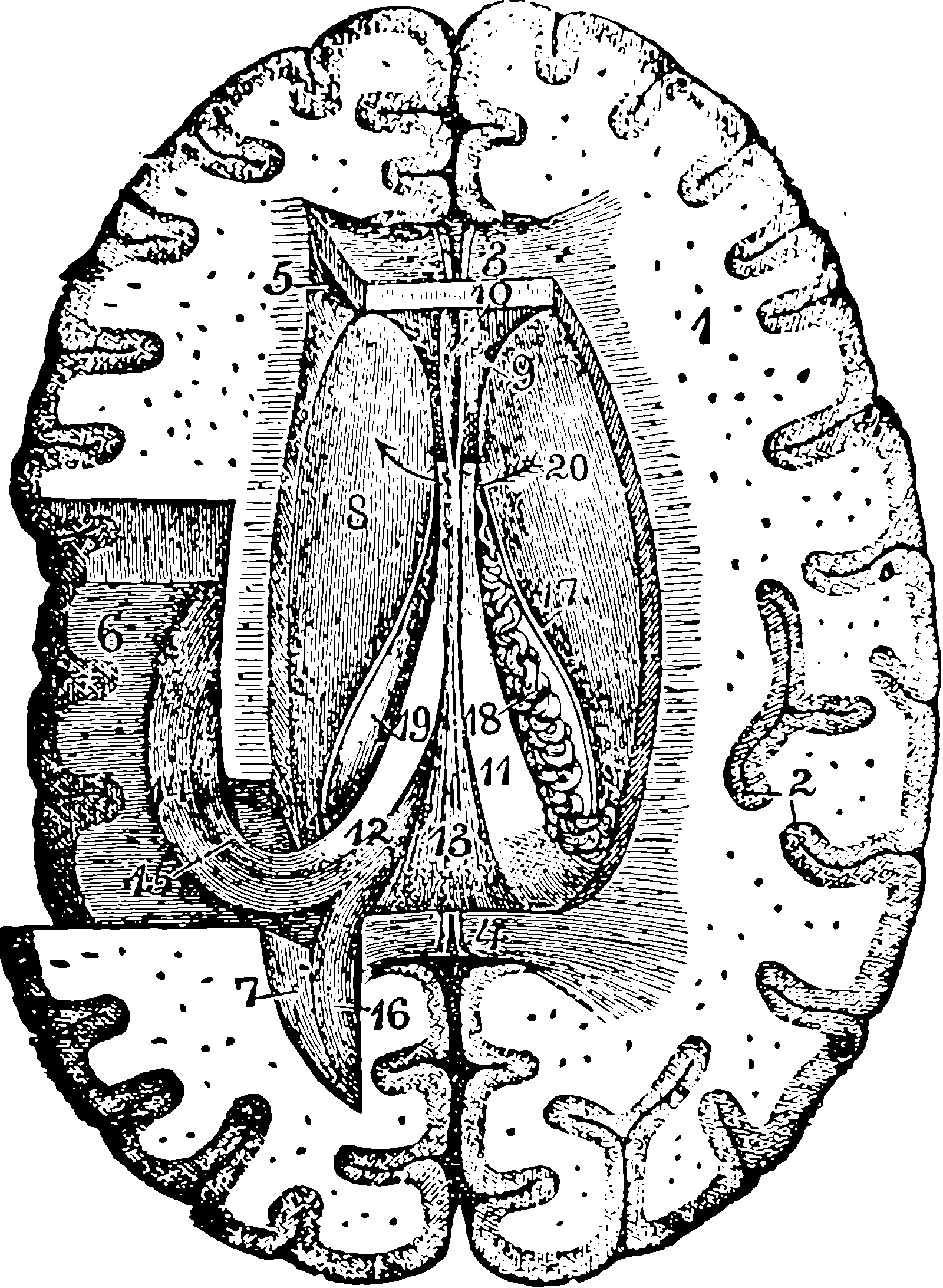
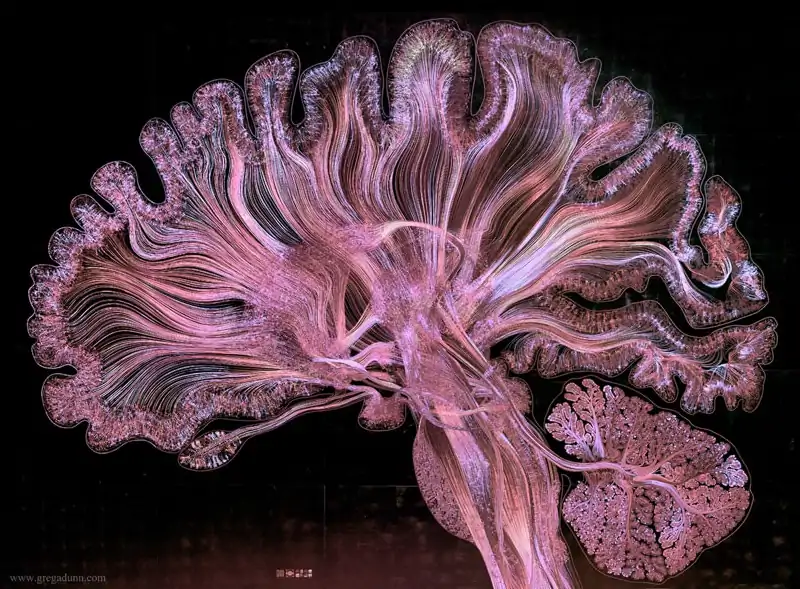
3 Pretty pictures of neurons
The names I am looking for here for beautiful hand-drawn early neuron diagrams are Camillo Golgi and Santiago Ramón y Cajal, especially the latter.