Deep generative models wat

1 What Does “Generative” Even Mean Any More?

Generative neural nets have upset the apple cart. When I was a baby Bayesian, the term “generative model” meant something very specific: a model that could generate samples from a probability distribution, often with a focus on understanding the underlying data-generating process: you’d posit some probability distribution, $P(x|\theta )$, that you believe your data $x$ is drawn from, given some parameters $\theta$. Then you’d often think about priors $P(\theta )$ and posteriors $P(\theta —x)$. The game was about defining and then “knowing” these distributions, or at least being able to sample from them in a way that respected their mathematical form. We wanted to characterize the underlying probabilistic process.

However, various things are hard about that Precise Bayesian inference, especially for complex models, can be extraordinarily challenging. For certain problems, computing exact posteriors or even expectations under them can be computationally intractable (e.g., falling into complexity classes like #P-hard (Daniel M. Roy 2011)). If we’re operating in an M-open setting—where we don’t even assume our chosen model class contains the true data-generating process—then striving for an exact Bayesian solution for our inevitably misspecified model might be an academic diversion rather than an actual solution to our problem.

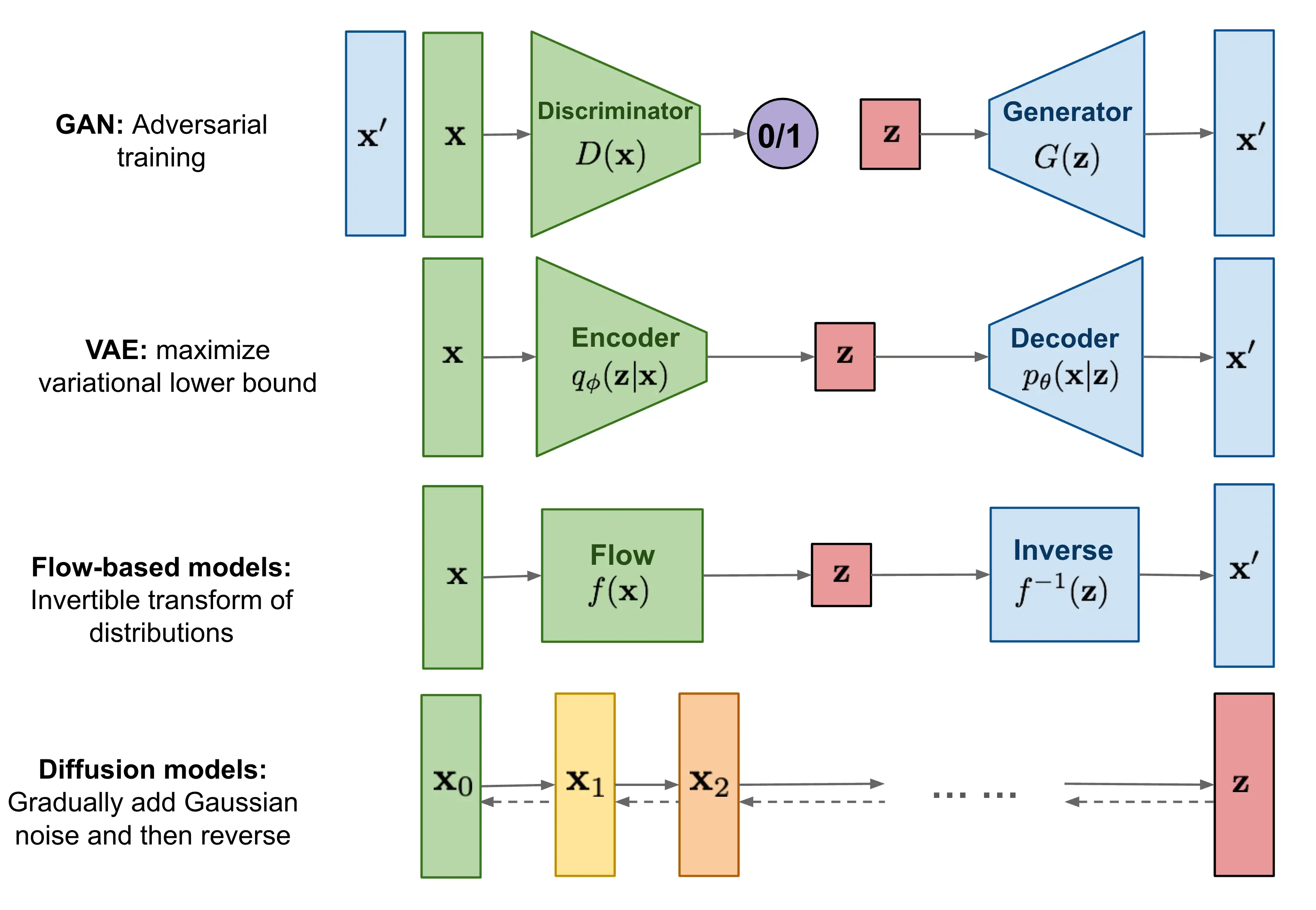
Generative NNs circumvent this problem by largely ignoring it. Here, let me sketch a kind of ziggurat of ignoringness, from the most traditional to the most modern. Variational methods like VAEs which still aim for likelihoods, often via an Evidence Lower Bound or ELBO. Implicit Variational Inference gives up on directly minimising ELBO. Then GANs give up all hope of likelihoods, and just think about fooling an adversary. Newer models like neural diffusion, Transformers used generatively, and the intriguing deep flow matching approaches still talk about input and output densities but they use them so obliquely that it is hard to case they use them as likelihood-type inference. Sure the set of all picture might have a “score function” but is really something about catpix densities, or a crutch for justifying the generative process to our Bayes-addled monkey brains?

Even within the variational family, we see a begrudgingly progression of increasingly relaxed interpretation in exchange for generative power. Deep Variational Bayes pushes the boundaries by learning complex, neural network-parameterized approximate posteriors, still very much striving for a coherent probabilistic interpretation of the system. Further along this path, Generalized Variational Inference allows approximating posteriors with respect to more general loss functions, not just the KL divergence which for some reason everyone got hooked on in standard VI.. There is still some kind of probabilistic interpretation but it doesn’t look familiar.

tl;dr **cutting-edge generative techniques have stumbled into the realization that explicitly wrestling with any well-defined posterior $P(\theta —x)$ or even a global $P(x)$ might be… overkill for the primary goal of producing more stuff that looks like $x$.

When we say generative it is to flag that we’re less obsessed with the platonic ideal of the posterior density and more focused on whether the samples our models produce “look like the real thing”. Can a discriminator tell them apart? Do they capture the texture, the structure, the je ne sais quoi of the training data? The weird thing for me is that even though this vague problem, je-ne-sais-quoi-hunting sounds like it is underspecified and thus way harder, it can end up being easier.

Kleinberg and Mullainathan (2024) make this precise for LLMs. They investigate language generation; the parallel to broader generative modeling is left as an exercise. Learning languages is known by any standard measures, to be what we refer to technically as gob smackingly hard. Their work suggests that generating new, valid strings from an unknown language (that is, samples from a distribution) can be achieved “in the limit” even when identifying the true underlying language (the exact distribution) is provably intractable. It’s a formal way of saying that producing plausible outputs doesn’t necessarily require a perfect internal model of the entire data-generating process. This is the kind of phenomenon we see all over the place in practice. Our models get good at generating stuff without necessarily understanding the probability distributions in the way a classical statistician might demand recognise as “understanding”.

The broader paradigm of Implicit Generative Models (IGMs), where GANs are a prime example, and the rise of score-based models like denoising diffusions, also fit here. These approaches often bypass an explicit, normalized likelihood function, focusing instead on directly learning a transformation from a simple noise distribution to the data distribution, or learning the gradients of the data log-density, or a discriminator or whatever. The success of these methods further suggests that direct generation, or learning the local structure (scores), might be a more tractable target than full density estimation.

So, when are these paradigms — the classical “know the distribution” and the modern “just make good samples” – actually the same thing? And when do they diverge? If my model can generate perfect samples, does it actually “know” the “distribution” in all the ways that matter? Do I gain nothing by attempting to understand the algorithm as a coherent probabilistic world model in the traditional sense?

2 What is Conditioning in Generative Models?

The likelihood interpretation is more of a load-bearing concern when we start thinking about conditioning in these generative processes, generating outputs consistent with an instruction or an observation. Conditioning is the bread and butter of Bayes. But, if we’ve relaxed our grip on explicit probability densities like $P(x,y)$ or $P(x—y)$, how do we now steer these generative processes? How do we say, “Generate an image of a cat, given that the prompt was ‘a fluffy feline sunbathing’?” Or, “Complete this sentence in the style of Shakespeare?” Current methods often involve clever conditioning tricks during training, guiding the diffusion process, or manipulating latent spaces, but it feels like we’re still figuring out the most principled ways to do this when the underlying probabilistic machinery is more implicit. When we are on the cusp of probabilistic and purely generative, as with diffusion models, it is possible to devise a conditioning method but it’s… weird.

Perhaps this is where ideas like learning latent representations and even world models come into play. If a model learns a rich, well-structured latent space, maybe that space itself acts as a kind of compressed, implicit representation of the data’s underlying structure, allowing for both generation and controlled manipulation without ever writing down $P(x)$. I’m inclined to think about those models as learning also to condition a conditioned process.

3 Probability is Still a Weird Abstraction, Maybe Weirder Now

Learning problems often involve juggling derivatives and integrals to measure how well we’ve approximated the world. Probabilistic neural nets combine Monte Carlo (for the integrals we can’t solve analytically) and auto-diff (for the derivatives) and use of either of these is very smooth on modern hardware with modern algorithms.

From this viewpoint, deep generative models are often solving an intractable integral (the one defining $P(x)$) by simulating samples probabilistically from something that behaves like it, in lieu of directly computing with that continuous, unknowable, intractable beast. But that continuous integral was always a bit of a contrivance, wasn’t it? A mathematician’s dream of a world filled with Platonic probability densities.

The world we inhabit doesn’t hand us probability densities; it hands us observations. The density is the abstraction we impose. So, it used to look odd when we talked about solving integrals by looking at data. Now, perhaps it’s even odder: we’re generating data that mimics the (imagined) output of an integral, without necessarily “solving” the integral or even fully defining the function being integrated. We’re chasing the behaviour of the distribution, not the distribution itself. Is this progress, or just a sophisticated way to admit defeat on the original, harder problem? Or is it, as Kleinberg and Mullainathan suggest for language, a fundamentally different and more achievable goal?

4 Further reading

Implicit variational inference is a related topic, where we learn a generative model without The core idea here is aligned with our broader theme: the approximate posterior, $q(\theta )$, doesn’t need to have an analytically tractable probability density function. Instead, $q(\theta )$ can be implicit, defined by a (potentially complex) generative neural network that transforms simple noise $ϵ$ into samples $\theta =g(ϵ)$. We can sample from $q$, but we might not be able to write down $q(\theta )$ itself.

5 References