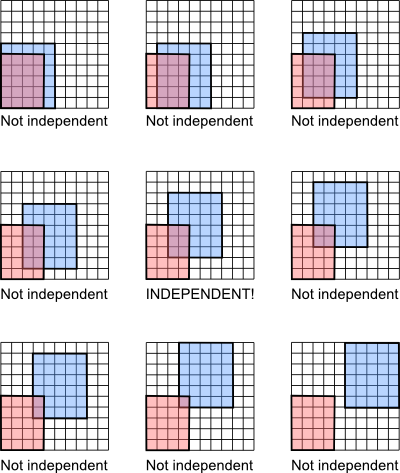
Independence, conditional, statistical
April 21, 2016 — September 13, 2020
Conditional independence between random variables is a special relationship. As seen in inference directed graphical models.
Connection with model selection, in the sense that accepting enough true hypotheses leaves you with a residual independent of the predictors. (🚧TODO🚧 clarify.)
1 As an algebra
The “graphoid axioms” (Dawid 1979, 1980)
\[\begin{aligned} \text{Symmetry: } & (X \perp\!\!\!\perp Y \mid Z) \implies (Y \perp\!\!\!\perp X \mid Z) \\ \text{Decomposition: } & (X \perp\!\!\!\perp YW \mid Z) \implies (X \perp\!\!\!\perp Y \mid Z) \\ \text{Weak union: } & (X \perp\!\!\!\perp YW \mid Z) \implies (X \perp\!\!\!\perp Y \mid ZW) \\ \text{Contraction: } & (X \perp\!\!\!\perp Y \mid Z) \,\wedge\, (X \perp\!\!\!\perp W \mid ZY)\implies (X \perp\!\!\!\perp YW \mid Z) \\ \text{Intersection: } & (X \perp\!\!\!\perp W \mid ZY) \,\wedge\, (X \perp\!\!\!\perp Y \mid ZW)\implies (X \perp\!\!\!\perp YW \mid Z) \\ \end{aligned}\] tell us what operations independence supports (nb the Intersection axiom requires that there are no probability zero events). If you map all the independence relationships between some random variables you are doing graphical models.
2 Tests
In parametric models we can say that if you don’t merely want to know whether two things are dependent, but how dependent they are, you may want to calculate a probability metric between their joint and product distributions. In the case of empirical observations and nonparametric independence this is presumably between the joint and product empirical distributions. If the distribution of the empirical statistic
2.1 Traditional tests
There are special cases where this is easy, e.g. in binary data we have χ² tests; for Gaussian variables it’s the same as correlation, so the problem is simply one of covariance estimates. Generally, likelihood tests can easily give us what is effectively a test of this in estimation problems in exponential families. (c&c Basu’s lemma.)
3 Chatterjee ξ
Modernized Spearman ρ. Looks like a contender as a universal replacement for a measure of (strength of) dependence (Azadkia and Chatterjee 2019; Chatterjee 2020). There seems to be a costly scaling of \(n \log n\) or even \(n^2\) in data size? Not clear. The method is remarkably simple (see the source code).
TODO: Deb, Ghosal, and Sen (2020) claims to have extended and generalised this and unified it with Dette, Siburg, and Stoimenov (2013).
3.1 Copula tests
If we know the copula and variables are monotonically related we know the dependence structure already. Um, Dette, Siburg, and Stoimenov (2013). Surely there are others?
3.2 Information criteria
Information criteria effectively do this. (🚧TODO🚧 clarify.)
3.3 Kernel distribution embedding tests
I’m interested in the nonparametric conditional independence tests of Gretton et al. (2008), using kernel tricks, although I don’t quite get how you conditionalize them.
RCIT (Strobl, Zhang, and Visweswaran (2017)) implements an approximate kernel distribution embedding conditional independence test via kernel approximation:
Constraint-based causal discovery (CCD) algorithms require fast and accurate conditional independence (CI) testing. The Kernel Conditional Independence Test (KCIT) is currently one of the most popular CI tests in the non-parametric setting, but many investigators cannot use KCIT with large datasets because the test scales cubicly with sample size. We therefore devise two relaxations called the Randomized Conditional Independence Test (RCIT) and the Randomized conditional Correlation Test (RCoT) which both approximate KCIT by utilising random Fourier features. In practice, both of the proposed tests scale linearly with sample size and return accurate p-values much faster than KCIT in the large sample size context. CCD algorithms run with RCIT or RCoT also return graphs at least as accurate as the same algorithms run with KCIT but with large reductions in run time.
4 Stein Discrepancy
Kernelized Stein Discrepancy is also IIRC a different kernelized test.