TODO: I should return to this and talk about the DAG here entirely in terms of marginalisation and conditionalisation operations. I think that would be clearer.
See also a previous version, and the notebook on causal inference this will hopefully inform one day.
We follow Pearl’s summary (Pearl 2009a), sections 1-3.
In particular, the paper surveys the development of mathematical tools for inferring (from a combination of data and assumptions) answers to three types of causal queries: (1) queries about the effects of potential interventions, (also called “causal effects” or “policy evaluation”) (2) queries about probabilities of counterfactuals, (including assessment of “regret,” “attribution” or “causes of effects”) and (3) queries about direct and indirect effects (also known as “mediation”)
In particular, I want to get to the identification of causal effects given an existing causal graphical model from observational data with unobserved covariates via criteria such as the back-door criterion. We’ll see. The approach is casual, motivating Pearl’s pronouncements without deriving everything from axioms. Will make restrictive assumptions to reduce complexity of presentation. Some concerns (e.g. over what we take as axioms and what as theorems) will be ignored.
Not covered: UGs, PDAGs, Maximal Ancestral Graphs…
Motivational examples
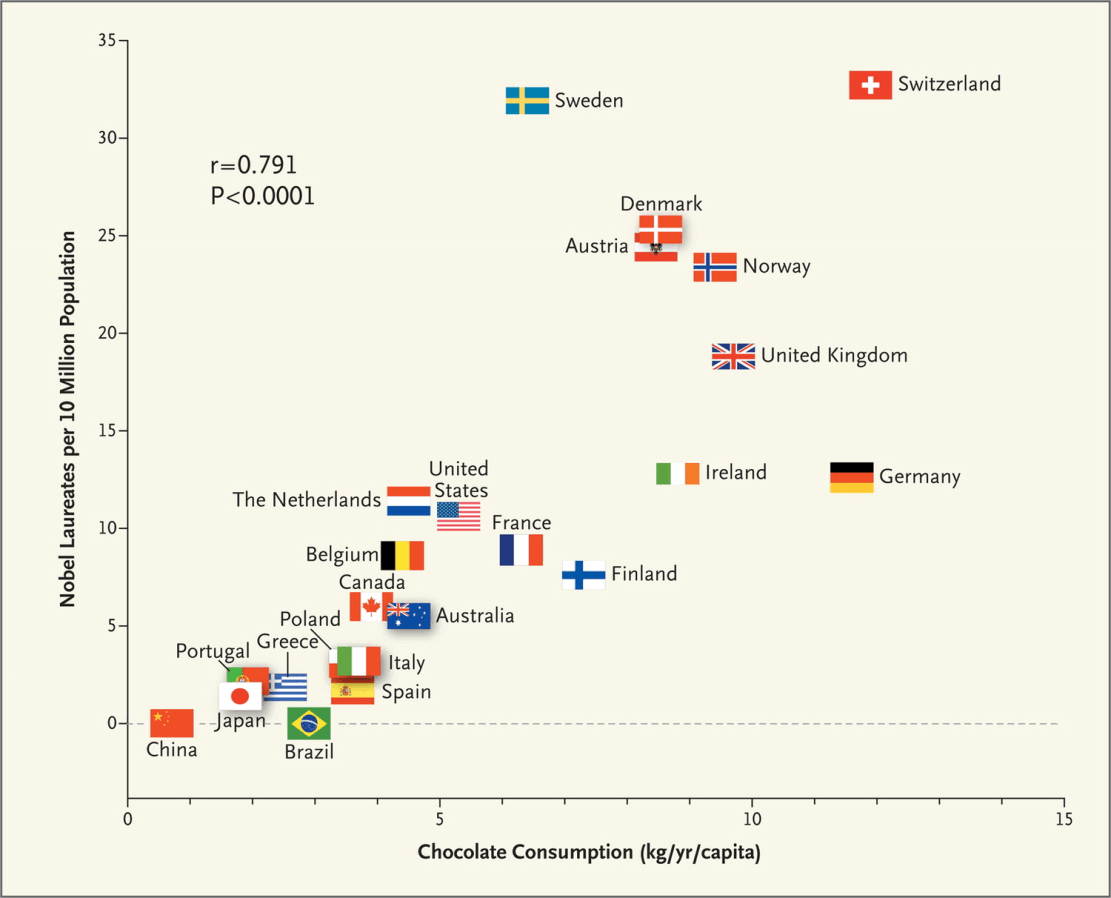
- Does chocolate cause you to get Nobel prizes? (Messerli 2012)
- Does hydroxychloroquine reduce COVID-19 death rate?
- Can we learn semantic objects from video? (Li et al. 2020)
- How do our weather-dependent models generalise to a changed climate? How does our in-house trained model generalise to messy real-world data? (Subbaswamy, Schulam, and Saria 2019)
- …
Generally
- Learning physical systems where we cannot do experiments
- Learning physical systems where someone else is intervening
- Generalising ML to out-of-sample conditions
- Learning the costs of outcomes that we do not observe
- Identify spurious inference from uncontrolled correlation
Graphical causal inference is the best-regarded tool to solve these problems (or at least, tell us when we can hope to solve these problems, which is not always.)
Machinery
We are interested in representing influence between variables in a non-parametric fashion.
Our main tool to do this will be conditional independence DAGs, and causal use of these. Alternative name: “Bayesian Belief networks”.1
Structural Equation Models
We have a finite collections of random variables \(\mathbf{V}=\{X_1, X_2,\dots\}\).
For simplicity of exposition, each of the RVs will be discrete so that we may work with pmfs, and write \(p(X_i|X_j)\) for the pmf. I sometimes write \(p(x_i|x_j)\) to mean \(p(X_i=x_i|X_j=x_j)\).
Extension to continuous RVs, or arbitrary RVs, is straightforward for everything I discuss here. (A challenge is if the probabilities are not all strictly positive on joint cdfs.)
Here is an abstract SEM example. Motivation in terms of structural models: We consider each RV \(X_i\) as a node and introduce a non-deterministic noise \(\varepsilon_i\) at each node. (Figure 3 in the Pearl (2009a))
\[\begin{aligned} Z_1 &= \varepsilon_1 \\ Z_2 &= \varepsilon_2 \\ Z_3 &= f_3(Z_1, Z_2, \varepsilon_3) \\ X &= f_X(Z_1, Z_3, \varepsilon_X) \\ Y &= f_Y(X, Z_2, Z_3, \varepsilon_Y) \\ \end{aligned}\]
Without further information about the forms of \(f_i\) or \(\varepsilon_i\), our assumptions have constrained the conditional independence relations to permit a particular factorization of the mass function:
\[\begin{aligned} p(x, y, z_3, z_2, z_1) = &p(z_1) \\ &\cdot p(z_2) \\ &\cdot p(z_3|z_1, z_2) \\ &\cdot p(x|z_1,z_2) \\ &\cdot p(y|x,z_2,z_3) \\ \end{aligned}\]
We would like to know which variables are conditionally independent of others, given such a factorization.
More notation. We write
\[ X \perp Y|Z \] to mean “\(X\) is independent of \(Y\) given \(Z\)”.
We use this notation for sets of random variables, and bold them to emphasis this.
\[ \mathbf{X} \perp \mathbf{Y}|\mathbf{Z} \]
We can solve these questions via a graph formalism. That’s where the DAGs come in.
Directed Acyclic Graphs (DAGs)
A DAG is graph with directed edges, and no cycles. (you cannot return to the same starting node travelling only forward along the arrows.)
Has an obvious interpretation in terms of causal graphs. Familiar from structural equation models.
Figure 1: The causal DAG of our abstract SEM example
DAGs are defined by a set of vertexes and (directed) edges.
\[ \mathcal{G}=(\mathbf{V},E) \]
We show the directs of edges by writing them as arrows.
For nodes \(X,Y\in \mathbf{V}\) we write \(X \rightarrow Y\) to mean there is a directed edged joining them.
We need some terminology.
- Parents
- The parents of a node \(X\) in a graph are all nodes joined to it by an incoming arrow, \(\operatorname{parents}(X)=\{Y\in \mathbf{V}:Y\rightarrow X\}.\) For convenience, we define \(X\in\operatorname{parents}(X)\)
- Children
- similarly, \(\operatorname{children}(X)=\{Y\in \mathbf{V}:X\rightarrow Y\}.\)
- Co-parent
- \(\operatorname{coparents}(X)=\{Y\in \mathbf{V}:\exists Z\in \mathbf{V} \text{ s.t. } X\rightarrow Z\text{ and }Y\rightarrow Z\}.\)
Ancestors and descendants should be clear as well.
This proceeds in 3 steps
The graphs describe conditional factorization relations.
We do some work to construct from these relations some conditional independence relations, which may be read off the graph.
From these relations plus a causal interpretation we derive rules for identification of effects
Anyway, a joint distribution \(p(\mathbf{V})\) decomposes according to a directed graph \(G\) if we may factor it
\[ p(X_1,X_2,\dots,X_v)=\prod_{X=1}^v p(X_i|\operatorname{parents}(X_i)) \]
Uniqueness?
The Pearl-style causal graphs we draw are I-graphs, which is to say &independence* graphs. We are supposed to think of them not as the graph where every edge shows an effect, but as a graph where every missing edge shows there is no effect.
It would be tempting to suppose that a node is independent of its children given its parents or somesuch. But things are not so simple.
Questions:
- \(\text{Sprinkler}\perp \text{Rain}\)?
- \(\text{Sprinkler}\perp \text{Rain}|\text{Wet season}\)?
- \(\text{Sprinkler}\perp \text{Rain}|\text{Wet pavement}\)?
- \(\text{Sprinkler}\perp \text{Rain}|\text{Wet season}, \text{Wet pavement}\)?
We need new graph vocabulary and conditional independence vocabulary.
Axiomatic characterisation of conditional independence. (Pearl 2008; Steffen L. Lauritzen 1996).
Theorem: (Pearl 2008) For disjoint subsets \(\mathbf{W},\mathbf{X},\mathbf{Y},\mathbf{Z}\subseteq\mathbf{V}.\)
Then the relation \(\cdot\perp\cdot|\cdot\) satisfies the following relations:
\[\begin{aligned} \mathbf{X} \perp \mathbf{Z} |\mathbf{Y} & \Leftrightarrow & \mathbf{Z}\perp \mathbf{X} | \mathbf{Y} && \text{ Symmetry }&\\ \mathbf{X} \perp \mathbf{Y}\cup \mathbf{W} |\mathbf{Z} & \Rightarrow & \mathbf{X} \perp \mathbf{Y} \text{ and } \mathbf{X} \perp \mathbf{W} && \text{ Decomposition }&\\ \mathbf{X} \perp \mathbf{Y}\cup \mathbf{W} |\mathbf{Z} & \Rightarrow & \mathbf{X} \perp \mathbf{Y}|\mathbf{Z}\cup\mathbf{W} && \text{ Weak Union }&\\ \mathbf{X} \perp \mathbf{Y} |\mathbf{Z} \text{ and } \mathbf{X} \perp \mathbf{W}|\mathbf{Z}\cup \mathbf{Y} |\mathbf{Z} & \Rightarrow & \mathbf{X} \perp \mathbf{Y}\cup \mathbf{W}|\mathbf{Z} && \text{ Contraction }&\\ \mathbf{X} \perp \mathbf{Y} |\mathbf{Z}\cup \mathbf{W} \text{ and } \mathbf{X} \perp \mathbf{W} |\mathbf{Z}\cup \mathbf{Y} & \Rightarrow & \mathbf{X}\perp \mathbf{W}\cup\mathbf{Y} | \mathbf{Z} && \text{ Intersection } & (*)\\ \end{aligned}\]
(*) The Intersection axiom only holds for strictly positive distributions.
visual intuition of graph axioms (Pearl 2008)
How can we relate this to the topology of the graph?
B in a fork path
B in a chain path
B in a collider path
Definition: A set \(\mathbf{S}\) blocks a path \(\pi\) from X to Y in a DAG \(\mathcal{G}\) if either
There a node \(a\in\pi\) which is not a collider on \(\pi\) such that \(a\in\mathbf{S}\)
There a node \(b\in\pi\) which is a collider on \(\pi\) and \(\operatorname{descendants}(b)\cap\mathbf{S}=\emptyset\)
If a path is not blocked, it is active.
Definition: A set \(\mathbf{S}\) d-separates two subsets of nodes \(\mathbf{X},\mathbf{X}\subseteq\mathcal{G}\) if it blocks every path between any every pair of nodes \((A,B)\) such that \(A\in\mathbf{X},\, B\in\mathbf{Y}.\)
This looks ghastly and unintuitive, but we have to live with it because it is the shortest path to making simple statements about conditional independence DAGs without horrible circumlocutions, or starting from undirected graphs, which is tedious.
Theorem: (Pearl 2008; Steffen L. Lauritzen 1996). If the joint distribution of \(\mathbf{V}\) factorises according to the DAG \(\mathbf{G}\) then for two subsets of variables \(\mathbf{X}\perp\mathbf{Y}|\mathbf{S}\) iff \(\mathbf{S}\) d-separates \(\mathbf{X}\) and \(\mathbf{Y}\).
This puts us in a position to make more intuitive statements about the conditional independence relationships that we may read off the DAG.
Corollary: The DAG Markov property.
\[ X \perp \operatorname{descendants}(X)^C|\operatorname{parents}(X) \]
Corollary: The DAG Markov blanket.
Define
\[ \operatorname{blanket}(X):= \operatorname{parents}(X)\cup \operatorname{children}(X)\cup \operatorname{coparents}(X) \]
Then
\[ X\perp \operatorname{blanket}(X)^C|\operatorname{blanket}(X) \]
Causal interpretation
We have a DAG \(\mathcal{G}\) and a set of variables \(\mathbf{V}\) to which we wish to give a causal interpretation.
Assume
- The \(\mathbf{V}\) factors according to \(\mathcal{G}\)
- \(X\rightarrow Y\) means “causes” (The Causal Markov property)
- We additionally assume faithfulness, that is, that \(X\leftrightsquigarrow Y\) iff there is a path connecting them.
So, are we done?
We add the additional condition that
- all the relevant variables are included in the graph.
The BBC raised one possible confounding variable:
[…] Eric Cornell, who won the Nobel Prize in Physics in 2001, told Reuters “I attribute essentially all my success to the very large amount of chocolate that I consume. Personally I feel that milk chocolate makes you stupid… dark chocolate is the way to go. It’s one thing if you want a medicine or chemistry Nobel Prize but if you want a physics Nobel Prize it pretty much has got to be dark chocolate.”
do-calculus
Now we can discuss the relationship between conditional dependence and causal effect. This is the difference between, say,
\[ P(\text{Wet pavement}|\text{Sprinkler}=on) \]
and
\[ P(\text{Wet pavement}|\operatorname{do}(\text{Sprinkler}=on)). \]
This is called “truncated factorization” in the paper. \(\operatorname{do}\)-calculus and graph surgery give us rules that allow us to calculate dependencies under marginalisation for intervention distributions.
If we know \(P\), this is relatively easy. Marginalize out all influences to the causal variable of interest, which we show graphically as wiping out a link.
Now suppose we are not given complete knowledge of \(P\), but only some of the conditional distributions. (there are unobservable variables). This is the setup of observational studies and epidemiology and so on.
What variables must we know the conditional distributions of in order to know the conditional effect? That is, we call a set of covariates \(\mathbf{S}\) an admissible set (or sufficient set) with respect to identifying the effect of \(X\) on \(Y\) iff
\[ p(Y=y|\operatorname{do}(X=x))=\sum_{\mathbf{s}} P(Y=y|X=x,\mathbf{S}=\mathbf{s}) P(\mathbf{S}=\mathbf{s}). \]
- Parent criterion
- The parents of a cause are an admissible set (Pearl 2009a).
- Back-door criterion
A set \(\mathbf{S}\) is sufficient if
- \(\mathbf{S}\cap\operatorname{descendants}(X)=\emptyset\)
- \(\mathbf{S}\) blocks all paths which start with an arrow into \(\mathbf{X}\)
There are other criteria.
Causal properties of sufficient sets:
\[ P(Y=y|\operatorname{do}(X=x),S=s)=P(Y=y|X=x,S=s) \]
Hence
\[ P(Y=y|\operatorname{do}(X=x),S=s)=\sum_sP(Y=y|X=x,S=s)P(S=s). \]
More graph transformation rules! But this time for interventions.
- Rule 1 (Insertion/deletion of observations)
- \(P(Y\mid \operatorname{do}(X),Z,W)=P(Y\mid \operatorname{do}(X),W)\) if \(Y\) and \(Z\) are d-separated by \(X\cup W\) in \(\mathcal{G}^*\), the graph obtained from \(\mathcal{G}\) by removing all arrows pointing into variables in \(X\).
- Rule 2 (Action/observation exchange)
- \(P(Y\mid \operatorname{do}(X),\operatorname{do}(Z),W)=P(Y\mid \operatorname{do}(X),Z,W)\) if \(Y\) and \(Z\) are d-separated by \(X\cup W\) in \(\mathcal{G}^{\dagger}\), the graph obtained from \(\mathcal{G}\) by removing all arrows pointing into variables in \(X\) and all arrows pointing out of variables in \(Z.\)
- Rule 3 (Insertion/deletion of actions)
- \(P(Y\mid \operatorname{do}(X),Z,W)=P(Y\mid \operatorname{do}(X),W)\) if \(Y\) and \(Z\) are d-separated by \(X\cup W\) in \(\mathcal{G}^{\ddagger}\), the graph obtained from \(\mathcal{G}\) by removing all arrows pointing into variables in \(X\) (thus creating \(\mathcal{G}^*\)) and then removing all of the arrows pointing into variables in \(Z\) that are not ancestors of any variable in \(W\) in \(\mathcal{G}^*.\)
If some causal effect of a DAG is identifiable, then there exists a sequence of application of the do-calculus rules that can identify causal effects using only observational quantities (Shpitser and Pearl 2008)
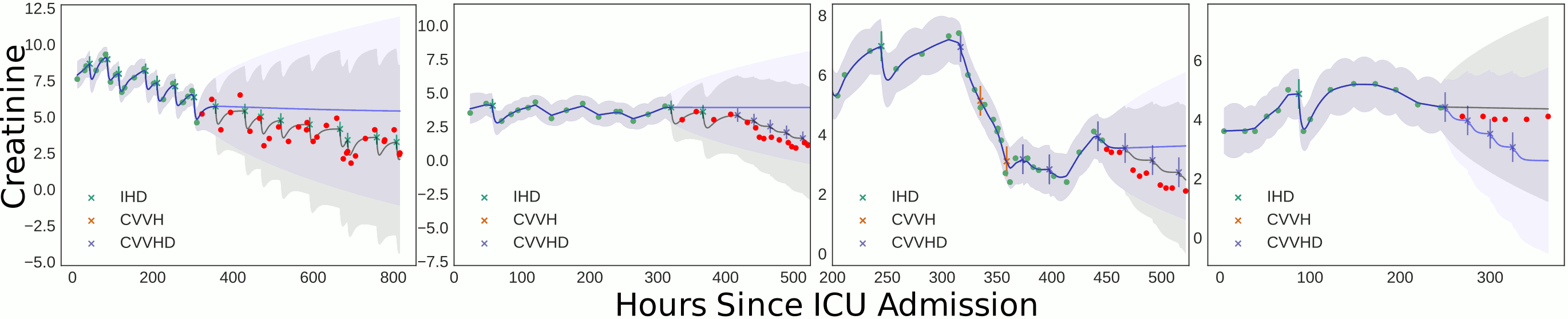
Case study: Causal GPs
Here is a cute paper (Schulam and Saria 2017) on causal Gaussian process regression. You need the supplement to the paper for it to make sense.
It uses Gaussian process regression to infer a time series model without worrying about discretization which is tricky in alternative approaches (e.g. Brodersen et al. (2015)).
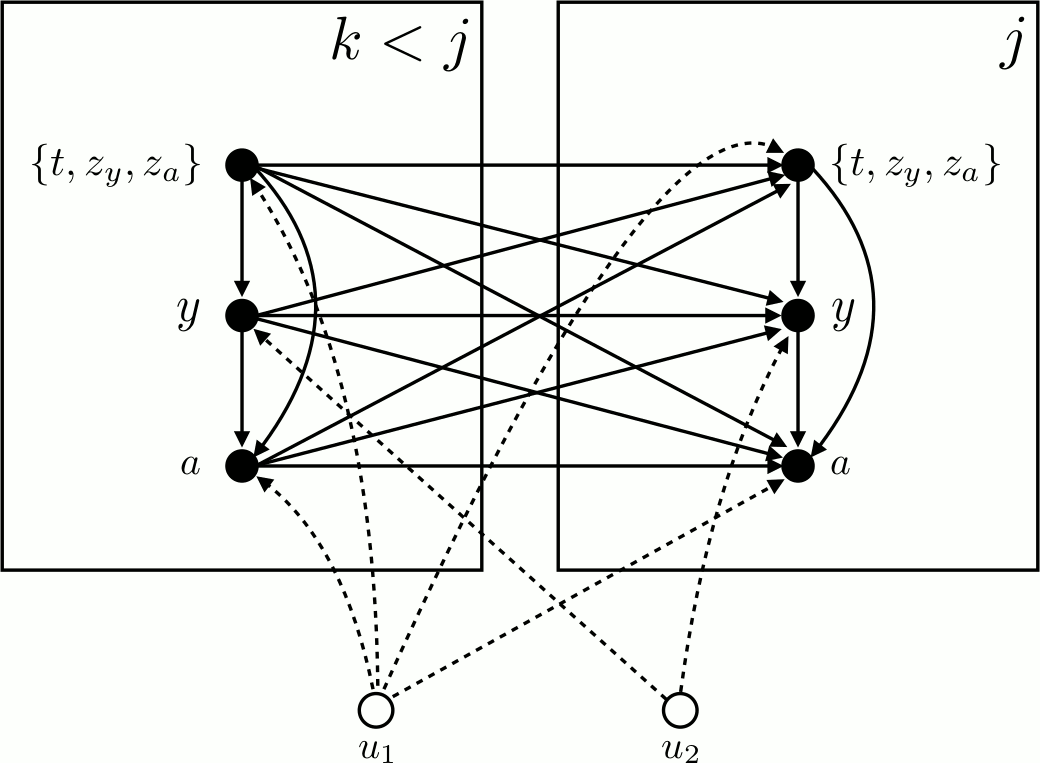
- (Consistency). Let \(Y\) be the observed outcome, \(A \in \mathcal{C}\) be the observed action, and \(Y[a]\) be the potential outcome for action \(a \in \mathcal{C},\) then: \((Y \triangleq Y[a]) \mid A=a\)
- (Continuous-Time NUC). For all times \(t\) and all histories \(\mathcal{H}_{t^{-}}\), the densities \(\lambda^{*}(t)\), \(p^{*}\left(z_{y}, z_{a} \mid t\right),\) and \(p^{*}\left(a \mid y, t, z_{a}\right)\) do not depend on \(Y_{s}[\) a \(]\) for all times \(s>t\) and all actions a.
- (Non-Informative Measurement Times). For all times t and any history \(\mathcal{H}_{t^{-}}\), the following holds: \(p^{*}\left(y \mid t, z_{y}=1\right) \mathrm{d} y=P\left(Y_{t} \in \mathrm{d} y \mid \mathcal{H}_{t^{-}}\right)\)
Schulam and Saria’s DAG
Notation decoder ring:
\[(Y[a]|X):= P(Y|X,\operatorname{do}(A=a)\]
What are unobserved \(u_1,u_2\)? Event and action models? Where are latent patience health states? \(u_2\) only effects outcome measurements. Why is there a point process at all? Does each patient possess a true latent class?
How does causality flow through GP?
Why is the latent mean 5-dimensional?
Recommended reading
Quick intros
- Mohan and Pearl’s 2012 tutorial
- Elwert’s intro (Elwert 2013)
- d-separation without tears is an interactive verson of Pearl’s original based on daggity, a graphical model digramming tool.
- Likewise, the ggdag bias structure vignette
shows of the useful explanation diagrams available in
ggdagand is also a good introduction to selection bias and causal dags themselves
Textbooks
People recommend me Koller and Friedman (2009), which includes many different flavours of DAG model and many different methods, but it didn’t suit me, being somehow too detailed and too non-specific at the same time.
Spirtes, Glymour, and Scheines (2001) and Pearl (2009a) are readable. Steffen L. Lauritzen (1996) is clear but the more general (partially directed graphs) and thus somewhat heavier. The shorter Steffen L. Lauritzen (2000) is good. Not overwhelming, once again starts with a slightly more general formalism (DAGs as a special case of PDAGs, moral graphs everywhere). Murphy (2012) has a minimal introduction intermingled with some related models, with a more ML, “expert systems”-flavour and more emphasis on Bayesian inference applications.
References
Terminology confusion: This is orthogonal to subjective probability.↩︎
No comments yet. Why not leave one?