Causal graphical model reading group 2022
Causal inference
2022-04-01 — 2022-04-28
Wherein Chapter 3 of Brady Neal’s course is recounted, potential outcomes are contrasted with causal DAGs, d-separation is developed to identify adjustment sets, and graphical rules are illustrated with example diagrams.
\[\renewcommand{\var}{\operatorname{Var}} \renewcommand{\corr}{\operatorname{Corr}} \renewcommand{\dd}{\mathrm{d}} \renewcommand{\vv}[1]{\boldsymbol{#1}} \renewcommand{\rv}[1]{\mathsf{#1}} \renewcommand{\vrv}[1]{\vv{\rv{#1}}} \renewcommand{\disteq}{\stackrel{d}{=}} \renewcommand{\gvn}{\mid} \renewcommand{\Ex}{\mathbb{E}} \renewcommand{P}{\mathbb{P}} \renewcommand{\indep}{\mathop{\perp\!\!\!\perp}}\]
My chunk (Chapter 3) of the internal reading group covering the Brady Neal course.
- Book title: Introduction to Causal Inference (Neal 2020)
- Book link (first 10 Chapters only)
- Course link (with slides and videos)
- This week’s bonus reading: Pearl (2018).
- See also
- the previous version, and
- the notebook on causal inference this will eventually inform.
0.1 Recap: potential outcomes
Last time we discussed the potential outcome framework, which answers the question: How do we calculate a treatment effect \(Y(t)\) for some treatment \(t\)? i.e. how do we calculate \[ \Ex[Y(1)-Y(0)]? \]
We used the following assumptions: \[\begin{aligned} (Y(1), Y(0))\indep T | X &\quad \text{Unconfoundedness}\\ Y = Y(t)&\quad \text{Consistency}\\ (Y(1), Y(0))\indep T&\quad \text{Overlap}\\ (Y(1), Y(0))\indep T&\quad \text{No interference}\\ \end{aligned}\]
Under those assumptions, we have the causal adjustment formula \[\Ex[Y(1) − Y(0)] = \Ex_{X}\left[ \Ex[Y | T{=}t, X] − \Ex[Y | T{=}s, X]\right]. \]
Aside: what is going on in positivity?
And now…
0.2 Graphical models for causation wrangling
We have a finite collection of random variables \(\mathbf{V}=\{X_1, X_2,\dots\}\).
For simplicity of exposition, each of the RVs will be discrete so that we may work with pmfs, and write \(P(X_i|X_j)\) for the pmf. I sometimes write \(P(x_i|x_j)\) to mean \(P(X_i=x_i|X_j=x_j)\).
More notation. We write \[ X \indep Y|Z \] to mean “\(X\) is independent of \(Y\) given \(Z\)”.
We can solve these questions via a graph formalism. That’s where the DAGs come in.
0.2.1 Directed Acyclic Graphs (DAGs)
A DAG is a graph with directed edges, and no cycles. (you cannot return to the same starting node travelling only forward along the arrows.)
DAGs are defined by a set of vertices and (directed) edges.
We show the directions of edges by writing them as arrows.
For nodes \(X,Y\in \mathbf{V}\) we write \(X \rightarrow Y\) to mean there is a directed edge joining them.
0.3 Bayesian networks
0.3.1 Local Markov assumption
Given its parents in the DAG, a node is independent of all its non-descendants.
With four variable example, the chain rule of probability tells us that we can factorize any \(P\) thus \[ P\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=P\left(x_{1}\right) P\left(x_{2} \mid x_{1}\right) P\left(x_{3} \mid x_{2}, x_{1}\right) P\left(x_{4} \mid x_{3}, x_{2}, x_{1}\right) \text {. } \]
If \(P\) is Markov with respect to the above graph then we can simplify the last factor: \[ P\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=P\left(x_{1}\right) P\left(x_{2} \mid x_{1}\right) P\left(x_{3} \mid x_{2}, x_{1}\right) P\left(x_{4} \mid x_{3}\right) . \]
If we further remove edges, removing \(X_{1} \rightarrow X_{2}\) and \(X_{2} \rightarrow X_{3}\) as the below figure,
Code
we can further simplify the factorization of \(P\) : \[ P\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=P\left(x_{1}\right) P\left(x_{2}\right) P\left(x_{3} \mid x_{1}\right) P\left(x_{4} \mid x_{3}\right) \]
0.3.2 Bayesian Network Factorization
Given a probability distribution \(P\) and a DAG \(G\), we say \(P\) factorizes according to \(G\) if \[ P\left(x_{1}, \ldots, x_{n}\right)=\prod_{i} P\left(x_{i} \mid \operatorname{parents}(X_i)\right). \]
0.3.3 Minimality
- Given its parents in the DAG, a node X is independent of all its non-descendants
- Adjacent nodes in the DAG are dependent.
0.4 Causal interpretation
0.4.1 Causal Edges
In a directed graph, every parent is a direct cause of all its children.
\(Y\) “directly causing“ \(X\) means that \(X=f(\operatorname{parent}(X),\omega)\) is a (stochastic) function of some parent set which includes \(Y,\) and some independent noise.
0.4.2 Causal Bayesian Networks
Causal Edges + Local Markov
0.5 Conditional independence in Bayesian networks
When we fix some nodes, which independences do we introduce?
0.5.1 Chains
\[P(a,b,c) = P(a)P(b|a)P(c|b)\]
We assert that, conditional on B, A and C are independent: \[ A\indep C | B \\ \Leftrightarrow\\ P(a,c|b) = P(a|b)P(c|b) \]
In slow motion, \[\begin{aligned} P(a,b,c) &= P(a)P(b|a)P(c|b)\\ P(a,c|b) &=\frac{P(a)P(b|a)P(c|b)}{P(b)}\\ &=P(c|b)\frac{P(a)P(b|a)}{P(b)}\\ &=P(c|b)\frac{P(a,b)}{P(b)}\\ &=P(c|b)P(a|b) \end{aligned}\]
0.5.2 Forks
\[P(a,b,c) = P(b)P(a|b)P(c|b)\]
We assert that, conditional on B, A and C are independent: \[ A\indep C | B \\ \Leftrightarrow\\ P(a,c|b) = P(a|b)P(c|b) \] In slow motion, \[\begin{aligned} P(a,b,c) &= P(b)P(a|b)P(c|b)\\ P(a,c|b) &=\frac{P(b)P(a|b)P(c|b)}{P(b)}\\ &=P(a|b)P(c|b) \end{aligned}\]
0.5.3 Immoralities
(Colliders, when I grew up.)
\[P(a,b,c) = P(b)P(c)P(a|b,c)\]
We assert that, conditional on B, A and C are not in general independent: \[ A \cancel{\indep} C | B \\ \Leftrightarrow\\ P(a,c|b) = P(a|b)P(c|b) \]
Proof that this never factorizes?
0.5.4 Blocked paths
A path between nodes \(X\) and \(Y\) is blocked by a (potentially empty) conditioning set \(Z\) if either of the following is true:
- Along the path, there is a chain \(\cdots \rightarrow W \rightarrow \cdots\) or a fork \(\cdots \leftarrow W \rightarrow \cdots\), where \(W\) is conditioned on \((W \in Z)\).
- There is a collider \(W\) on the path that is not conditioned on \((W \notin Z)\) and none of its descendants are conditioned on \((\operatorname{descendants}(W) \nsubseteq Z)\).
0.5.5 d-separation
Two (sets of) nodes \(\vv{X}\) and \(\vv{Y}\) are \(d\)-separated by a set of nodes \(\vv{Z}\) if all of the paths between (any node in) \(\vv{X}\) and (any node in) \(\vv{Y}\) are blocked by \(\vv{Z}\).
0.5.6 d-separation in Bayesian networks
We use the notation \(X \indep_{G} Y \mid Z\) to denote that \(X\) and \(Y\) are d-separated in the graph \(G\) when conditioning on \(Z\). Similarly, we use the notation \(X \indep_{P} Y \mid Z\) to denote that \(X\) and \(Y\) are independent in the distribution \(P\) when conditioning on \(Z\).
Given that \(P\) is Markov with respect to \(G\) if \(X\) and \(Y\) are d-separated in \(G\) conditioned on \(Z\), then \(X\) and \(Y\) are independent in \(P\) conditioned on \(Z\).
\[ X \indep_{G} Y |Z \Longrightarrow X \indep_{P} Y | Z. \]
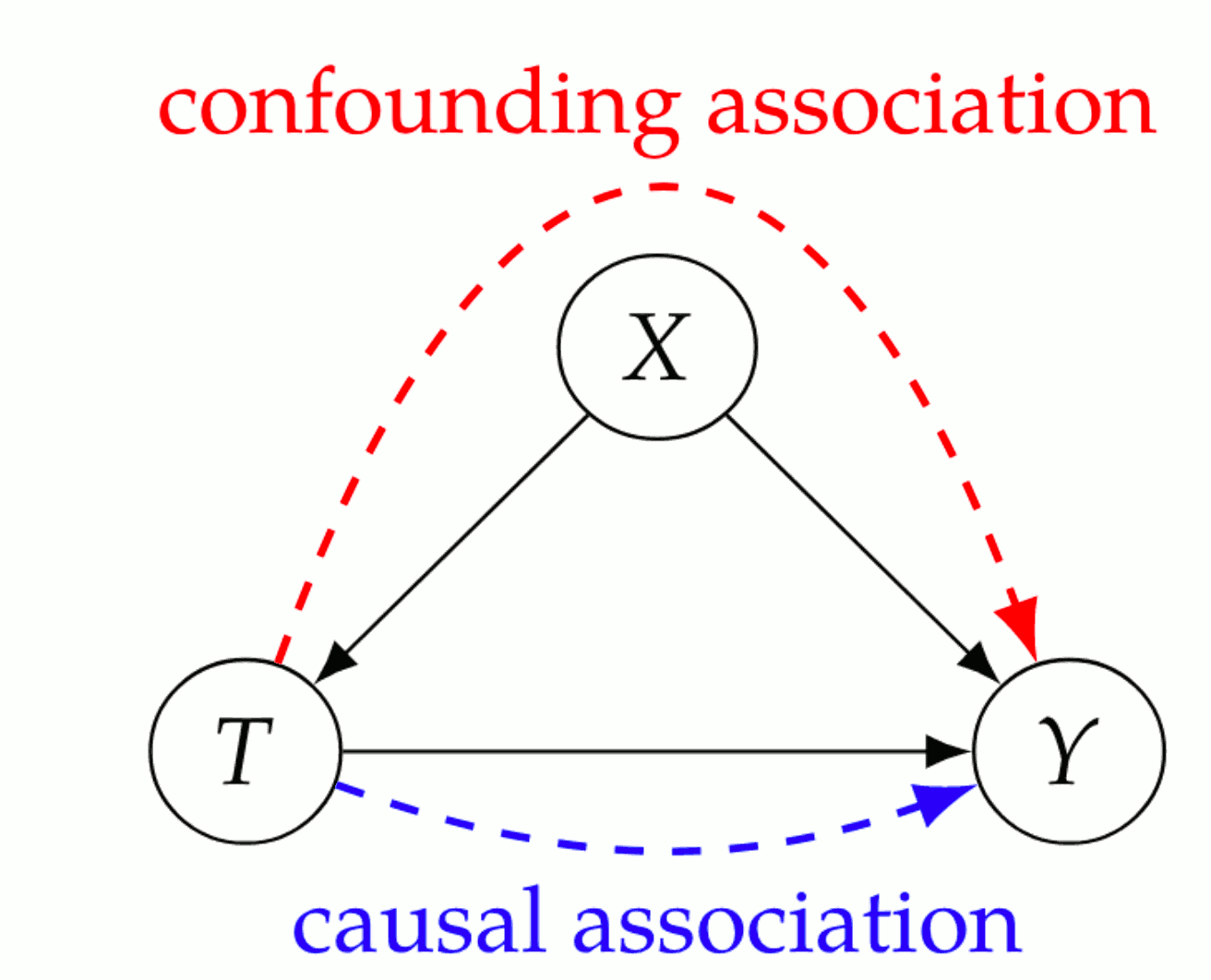
1 d-separation implies Association is Causation
1.1 Recommended reading
- Mohan and Pearl’s 2012 tutorial
- Elwert’s intro (Elwert 2013)
- d-separation without tears is an interactive version of Pearl’s original based on daggity.
- Likewise, the ggdag bias structure vignette shows off the useful explanation diagrams available in
ggdagand is also a good introduction to selection bias and causal dags themselves