Scientific machine learning
Machine learning for physical sciences, SciML
2017-05-15 — 2025-01-01
Wherein machine learning is employed to infer best-possible stochastic models of physical systems, ocean tracer dynamics and conservation laws are invoked as constraints, and surrogate PDE-informed networks are considered.
In physics, typically, we are concerned with identifying True Parameters for Universal Laws, applicable without prejudice across all the cosmos. We are hunting something like the Platonic ideals that our experiments are poor shadows of. Especially, say, quantum physics or cosmology.
In machine learning, typically we want to make generic predictions for a given process, and quantify how good those predictions can be given how much data we have and the approximate kind of process we witness, and there is no notion of universal truth waiting around the corner to back up our wild fancies. On the other hand, we are less concerned about the noisy sublunary chaos of experiments and don’t need to worry about how far our noise drives us from universal truth as long as we make good predictions in the local problem at hand. But here, far from universality, we have weak and vague notions of how to generalize our models to new circumstances and new noise. That is, in the Platonic ideal of machine learning, there are no Platonic ideals to be found.
(This explanation does no justice to either physics or machine learning, but it will do as framing rather than getting too deep into the history or philosophy of science.)
Can these areas have something to say to one another nevertheless? After an interesting conversation with Shane Keating about the difficulties of ocean dynamics, I am thinking about this in a new way; Generally, we might have notions from physics of what “truly” underlies a system, but where many unknown parameters, noisy measurements, computational intractability and complex or chaotic dynamics interfere with our ability to predict things using only known laws of physics; Here, we want to come up with a “best possible” stochastic model of a system given our uncertainties and constraints, which looks more like an ML problem.
At a basic level, it’s not controversial (I don’t think?) to use machine learning methods to analyse data in experiments, even with trendy deep neural networks. I understand that this is significant, e.g. in connectomics.
Perhaps a little more fringe is using machine learning to reduce computational burden via surrogate models, e.g. Carleo and Troyer (2017).
The thing that is especially interesting to me right now is learning the whole model in ML formalism, using physical laws as input to the learning process.
To be concrete, Shane specifically was discussing problems in predicting and interpolating “tracers”, such as chemical or heat, in oceanographic flows. Here we know lots of things about the fluids concerned, but less about the details of the ocean floor and have imperfect measurements of the details. Nonetheless, we also know that there are certain invariants, conservation laws etc, so a truly “nonparametric” approach to dynamics is certainly throwing away information.
There is some nifty work in learning symbolic approximations to physics, like the SINDy method. However, it’s hard to imagine scaling this up (at least directly) to big things like large image sensor arrays and other such weakly structured input.
Researchers like Chang et al. (2017) claim that learning “compositional object” models should be possible. The compositional models are learnable objects with learnable pairwise interactions, and bear a passing resemblance to something like the physical laws that physics experiments hope to discover, although I’m not yet totally persuaded about the details of this particular framework. On the other hand, unmotivated appealing to autoencoders as descriptions of underlying dynamics of physical reality doesn’t seem sufficient.
There is an O’Reilly podcast and reflist about deep learning for science in particular. There was a special track for papers in this area in NeurIPS.
See various SciML conferences, e.g. ICERM
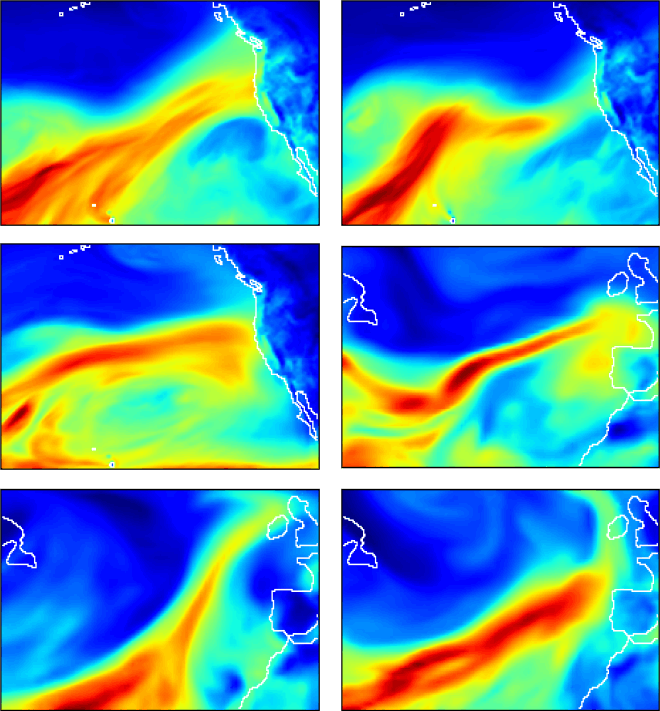
Sample images of atmospheric rivers correctly classified (true positive) by our deep CNN model. Figure shows total column water vapor (colour map) and land sea boundary (solid line). Y. Liu et al. (2016)
1 Data-informed inference for physical systems
See Physics-based Deep Learning (Thuerey et al. 2021). Also, see Brunton and Kutz’s Data-Driven Science and Engineering web material around their book (Brunton and Kutz 2019). Also, the seminar series by the authors of that latter book is a moving feast of the latest results in this area. For neural dynamics in particular, Patrick Kidger’s thesis seems good (Kidger 2022).
2 ML for PDEs
I do a lot of ML for PArtial Differential Equations. For more on that, see ML PDEs.
3 ML for biology
I think we call this BioML.
4 Causality, identifiability, and observational data
One ML-flavoured notion is the use of observational data to derive the models. Presumably if I am modelling an entire ocean or even river, doing experiments is out of the question for reasons of cost and ethics, and the overall model will be calibrated with observational data. We need to wait until there is a flood to see what floods do. This is generally done badly in ML, but there are formalisms for it, as seen in graphical models for causal inference. Can we work out the confounders and do counterfactual inference? Is imposing an arrow of causation already doing some work for us?
Small subsystems might be informed by experiments, of course.
5 Likelihood free inference
Popular if you have a simulator that can simulate from the system. See likelihood free inference.
6 Emulation approaches
7 The other direction: What does physics say about learning?
See why does deep learning work or the statistical mechanics of statistics.
Related, maybe: the recovery phase transitions in compressed sensing.
8 But statistics is ML
Why not “statistics for physical sciences”? Isn’t ML just statistics? Why thanks, Dan, for asking that. Yes it is, as far as content goes. But the different disciplines licence different uses of the tools. Pragmatically, using predictive modelling tools that ML practitioners advocate has been helpful in doing better statistics for ML. When we talk about statistics in physical processes we tend to think of your grandpappy’s statistics, parametric methods where the parameters are the parameters of physical laws. The modern emphasis in machine learning is in nonparametric, overparameterised or approximate methods that do not necessarily correspond to the world in any interpretable way. Deep learning etc. But sure, that is still statistics if you like. I would have needed to spend more words explaining that though, and buried the lede.
9 Applications
10 Incoming
Pasteur-ISI’sTesseract-based Differentiable Programming for Physics system
Microsoft Research branded: AI4Science to empower the fifth paradigm of scientific discovery
Physics-constrained machine learning for scientific computing - Amazon Science
An Infinitesimal Introduction to Stochastic Differential Equation Modeling
Neuromancer SciML library | Ján Drgoňa
Neural Modules with Adaptive Nonlinear Constraints and Efficient Regularizations (NeuroMANCER) is an open-source differentiable programming (DP) library for solving parametric constrained optimization problems, physics-informed system identification, and parametric model-based optimal control. NeuroMANCER is written in PyTorch and allows for systematic integration of machine learning with scientific computing for creating end-to-end differentiable models and algorithms embedded with prior knowledge and physics.