Gaussian Ensemble Belief Propagation

1 The problems we want to solve

A classic example of such a problem can be seen in Figure 2. That diagram is a simplified representation of what scientists want to do when trying to use lots of different kinds of data to understand something big, in the form of a graphical model. In this case, it is a graphical model of the ocean and the atmosphere, the kind of thing which we need to do when we are modelling the planetary climate. An arrow \(X \rightarrow Y\) means (more or less) “\(X\) causes \(Y\)” or “\(X\) influences \(Y\)” We can read off the diagram things like “The state of the ocean on day 3 influence the state of the ocean on day 4 and also the state of the atmosphere on day 4”. We also know that we have some information about the state of the ocean on that day because it is recorded satellite photo, and some information about the atmosphere that same day from radar observations.

Now the question is: how can we put all this information together? If I know some stuff about the ocean on day 3, how much do I know about it on day 4? How much can I use my satellite images to update my information about the ocean? How much does that satellite photo actually tell me?

What we really want to do is exploit our knowledge of the physics of the system. Oceans are made of water, and we know a lot about water. We are pretty good at simulating water. “For a neat demonstration of fluid simulation, see Figure 3, showcasing work from our colleagues in Munich. You an run this on your home computer right now if you want.

The problem is that: when these simulators have all the information about the world they are not bad at simulating it. But in practice, we don’t know everything there is to know. The world is big and complicated and we are almost always missing some information. Maybe our satellite photos are blurry, or don’t have enough pixels, or a cloud wandered in front of the camera at the wrong moment, or any one of a thousand other things

Our goal in this paper is to leverage good simulators to get high fidelity understanding of complicated stuff even when we have partial, noisy information. There are a lot of problems we want to solve at once here: We want to trade off statistical difficulty, and computational difficulty, and we would like to leverage as much as we can the hard work of the scientists who have gone before us.

There is no silver bullet method that can solve this for every possible system; everything has trade-offs; we will need to choose something like ‘the best guess we can make given how much computer time we have’.

The reason that we care about problems like that is that basically anything at large scale involves this kind of problem. Power grids! Agriculture! Floods! Climate! Weather! Most things that impact the well-being of millions of people at once end up looking like this, and as such All of these important problems are difficult to get accurate results for, and it is slow to calculate solutions.

We think in GEnBP, we find good answers very cheaply for precisely this punishing problem.

2 Our solution

Our approach utilizes existing simulators, originally designed for full information, to make educated guesses about what is going on, by feeding in random noise to indicate our uncertainty. We check the outputs of this educated guess (the prior for statisticians following along at home). Then we make an update rule that uses the information we have to improve this guess, until we have squeezed all the information we can out of the observations.

How exactly we do this is not very complicated, but it is technical. Long story short— our method is in a family of called belief propagation methods, which tells us how to update our guesses when new information arrives. Moreover, this family updates our guesses using only local information, e.g. we only look at “yesterday” and “today” together rather than looking at all the days at once. We need to walk through all the data to do this, ideally many times, so it takes a while. Each time we try to squeeze more information out of the update.

That is not a new technique; people have been doing it for decades. Our trick is that we can use simulators to do it, rather than a complicated statistical model. To gauge the certainty of my input data, we run the simulator with various inputs and observe the outputs.

The minimum viable example for us, and the one we tackle in the paper, is a (relatively) simple test case, Figure 4. This is what’s known as a system identification problem. Each circle represents a variable (i.e. some quantity we want to measure, like the state of the ocean), and each arrow signifies a ‘physical process we can simulate’. The goal is to identify the query parameter (red circle) from the evidence, i.e. the some noisy observations we made of the system.

The data in this case comes from a fluid simulator, of are simply modelling a fluid flowing around a doughnut-shaped container. We didn’t collect actual data for this experiment, which is just as well—I’m a computer scientist, not a lab scientist 😉. Our observations are low-resolution, distorted, and noisy snapshots of the state of the fluid. That red circle indicates a hidden influence on the system; in our case it is force that “stirs” the fluid. Our goal is “can I work out what force is being applied to this fluid, by taking a series of photos of it?”

In fact, many modern methods ignore this hidden influence entirely; the Ensemble Kalman Filter, for example, struggles with hidden influences.. But in practice we care a lot about such hidden influence. For one thing, such hidden factors might be interesting in themselves. Sailors, for example, care not just about the ocean waves, but also with what the waves’s behaviour might indicate about underwater hazards. Also, we want to be able distinguish between external influences and the dynamics of a system itself, because, for example, we might want to work out how to influence the system. If I am careful about identifying which behaviour comes from some external factor, this lets me deduce what external pressure I need to apply to it myself. What if I want to not only work out how the water flows, but how it will flow when I pump more water in?

This challenge belongs to a broader field known as Causal inference from observational data, which concerns itself with unraveling such complexities. I feel that is probably worth a blog post on its own, but for now let us summarise it with the idea that a lot of us think it is important to learn what is actually going on underneath, rather than what only appears to be going on.

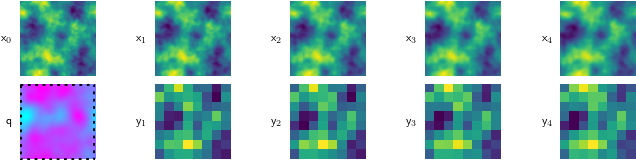
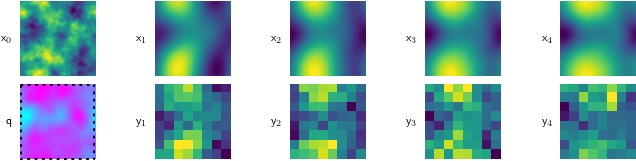
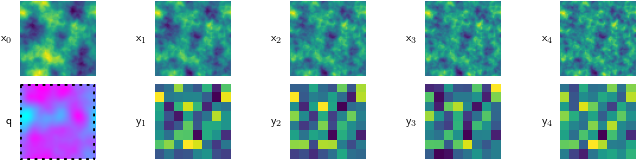
Because this is a simulated problem we can cheaply test our method against many different kinds of fluids, so we do, testing out thing on runny fluid, Figure 5 (a); and thick, viscous fluid, Figure 5 (c); and stuff in between, Figure 5 (b). For all of these the starting condition (\(\mathsf{x}_0\)) is the same and our goal is to find the magenta-tinted answer (\(\mathsf{q}\).)

3 Performance

Having outlined the problem, let’s now delve into the performance of GEnBP, our proposed solution. As a researcher, it’s essential to justify the efficacy of our methods How good is GEnBP, relatively speaking? As far as we can tell there is only one real competitor in this space, which is classic Gaussian Belief Propagation (GaBP) — more on GaBP below We use that as a baseline.

It’s challenging to present multiple simulations from a 2D fluid simulator effectively, as they primarily consist of colorful squares that are not immediately interpretable. This is easier if we can plot it in 1 spatial dimension. For demonstration purposes, I set up a special 1D pseudo-fluid simulator. The question, in this one, is “how well do our guesses about the influencing variable converge on the truth?”

The classic GaBP results Figure 6 are… OK I guess? In the figure, the red lines represent our initial educated guesses (‘prior’), and the blue lines show the optimized final guesses (‘posterior’), compared to the dotted black line representing the truth. The blue guesses are much better than the red one, for sure, but they are not amazing. Our fancy GEnBP guesses Figure 7 are way better, clustering much closer to the truth. So tl;dr on this very made-up problem, our method does way better at guessing the ‘hidden influence’ on the system.

This example is extremely contrived though! So let us quantify how much better the answers are on the more complex, more realistic, 2-dimensional problem.

At this stage, our approach manages millions of pixels, surpassing the capabilities of classical methods. GaBP tends to choke on a few thousand pixels. But our method can eat up big problems like that for breakfast.

What we are looking at in this graph is some measures of performance as we scale up the size of the problem, i.e. the number of pixels. The top graph displays the execution time, which ideally should be low, plotted against the problem size, measured in pixels. Notice that as the problem gets bigger GaBP gets MUCH slower — For the curious, it scales roughly cubically, i.e. \(\mathcal{O}(D^3)\). GaBP is always slower for the kind of problems we care about. Eventually, GaBP runs out of memory. In the middle graph we see something else interesting: GEnBP also has superior accuracy to the classic GaBP, in the selse that its guesses are closer to the truth. The bottom graph shows the posterior likelihood, which essentially tells us how confident our method is in the vicinity of the truth.

We have been strategic with our choice of problem here: GaBP is not amazing at fluid dynamics precisely like this, and that it kind of why we bother with this whole thing. GaBP has trouble with very nonlinear problems, which are generally just hard. GEnBP has some trouble with them too, but often much less trouble, and it can handle a much more diverse array of problems, especially ones with this geospatial flavour.

In Figure 9 we test both these methods on lot of different fluid types and see how they go. GEnBP is best at speed for … all of them. The story about accuracy is a little more complicated. We win some, and we lose some. So, it’s not a silver bullet.

However, GEnBP can tackle problems far beyond GaBP’s capacity, and it often superior accuracy even in scenarios manageable by GaBP.

4 How it works

The core insight of our work is combining the best elements of the Ensemble Kalman Filter (EnKF) and classic Gaussian belief propagation (GaBP). We’ve developed an alternative Gaussian belief propagation method that outperforms the classic GaBP. These methods are closely related and yet their research communities don’t seem to be closely connected. GaBP is associated with the robotics community. If you have a robotic vacuum cleaner, it probably runs on something like that. Rumour holds that the Google Street View software that makes all those Street View maps uses this algorithm. There are many great academic papers on it; here are some examples(Bickson 2009; Davison and Ortiz 2019; Murphy, Weiss, and Jordan 1999; Ortiz, Evans, and Davison 2021; Dellaert and Kaess 2017).

The Ensemble Kalman Filter is widely used in areas such as weather prediction and space telemetry. While I don’t have visually striking demos to share, I recommend Jeff Anderson’s lecture for a technical overview. Aside: Maybe if climate scientist could make their demos as sexy as the robotics folks, we would have more interest in climate modeling? Here are some neat introductory papers on that theme: (Evensen 2009a, 2009b; Fearnhead and Künsch 2018; Houtekamer and Zhang 2016; Katzfuss, Stroud, and Wikle 2016).

As far as work connecting those two fields, there does not seem to be much, even though they have a lot in common. That is where our GEnBP comes in. Our method is surprisingly simple, but it appears to be new, at least for some value of new.

Connecting the two methods is mostly a lot of “manual labour”. We use some cool tricks such as the Matheron update (Doucet 2010; Wilson et al. 2020, 2021), and a whole lot of linear algebra tricks such as Woodbury identities. Details in the paper.

5 Try it yourself

Code for GEnBP can be found at danmackinlay/GEnBP. And of course, read the GEnBP paper (MacKinlay et al. 2024).

Development was supported by CSIRO Machine Learning and Artificial Intelligence Future Science Platform. The paper was an effort by many people, not just myself but also Russell Tsuchida, Dan Pagendam and Petra Kuhnert.

If you’d like to cite us, here is a convenient snippet of BibTeX:

@misc{MacKinlayGaussian2024,
  title = {Gaussian {{Ensemble Belief Propagation}} for {{Efficient Inference}} in {{High-Dimensional Systems}}},
  author = {MacKinlay, Dan and Tsuchida, Russell and Pagendam, Dan and Kuhnert, Petra},
  year = {2024},
  month = feb,
  number = {arXiv:2402.08193},
  eprint = {2402.08193},
  publisher = {arXiv},
  doi = {10.48550/arXiv.2402.08193},
  archiveprefix = {arxiv}
}

6 Appendix

Curious how fast this method is? Here is the speed-comparison table for experts:

Computational Costs for Gaussian Belief Propagation, Ensemble Belief propagation for node dimension \(D\), ensemble size/component rank \(N\).

7 References