Probabilistic programming
Doing statistics using the tools of computer science
2019-10-02 — 2025-10-06
Wherein probabilistic programming is presented as a means to express Turing‑complete generative models and to perform inference, with MCMC, variational methods and autodifferentiation being supplied.
Probabilistic programming languages (PPLs) are tools for expressing and working with probabilistic models. A probabilistic programming system specifies stochastic generative models and helps us reason about them. Or, as Fabiana Clemente puts it:
Probabilistic programming is about doing statistics using the tools of computer science.
The program represents our random generative model, and conditioning upon the observed data gives us updated distributions over parameters, predictions, or whatever. Typically this will automatically account for the graphical model structure.
By convention, when I say ‘probabilistic programming’ rather than merely inference, I mean to signal a certain ambition; I’m hoping my technique can do inference for complicated models, possibly ones without tractable likelihoods of any kind, maybe even Turing-complete models. Usually I wouldn’t say I was using a PPL for a garden-variety hierarchical model, because that isn’t ambitious enough. That simpler usage is also fine, though it might be regarded as an up-sell. Hope in this context means something like “we have the programming primitives to, in principle and perhaps approximately, express the awful, crazy likelihood structure of a complicated problem, and to do something that looks like it might estimate the correct conditional density, but for any given problem we’re on our own to show it actually solves the desired task to the required accuracy in the required time.”
Many of these tools use Markov Chain Monte Carlo sampling, which turns out to be a startlingly general way to grind out estimates of the necessary conditional probability distributions, especially if we don’t worry too much about convergence rates. Some frameworks enable other methods, such as classic conjugate priors for easy (sub-)models, variational methods of all stripes, including reparameterization flows, and many hybrids of all of the above.
See George Ho of PyMC3/PyMC4 for an in-depth introduction to what might be desirable when solving these problems in practice,
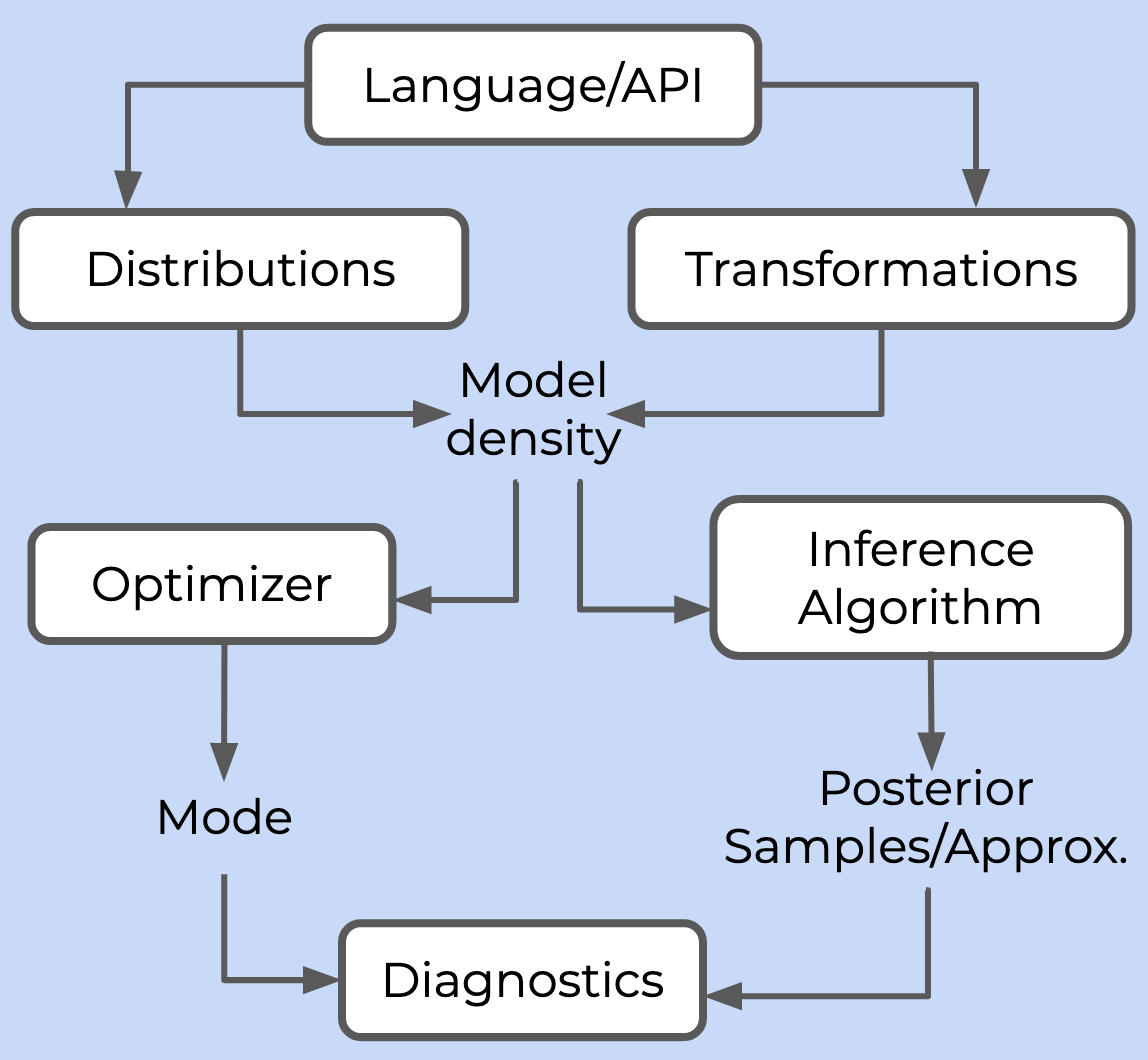
A probabilistic programming framework needs to provide six things:
- A language or API for users to specify a model
- A library of probability distributions and transformations to build the posterior density
- At least one inference algorithm, which either draws samples from the posterior (in the case of Markov Chain Monte Carlo, MCMC) or computes some approximation of it (in the case of variational inference, VI)
- At least one optimizer, which can compute the mode of the posterior density
- An autodifferentiation library to compute gradients required by the inference algorithm and optimizer
- A suite of diagnostics to monitor and analyse the quality of inference
See also Col Carroll’s overview of several trendy frameworks. This list omits some items I left out due to exhaustion and choice paralysis. Check the dates on all advice in this area; as a hip research topic, there is a constant flux of new frameworks in and out of use.
1 Tutorials and textbooks
With Tom Blau, I recently wrote a tutorial introduction to pyro, csiro-mlai/hackfest-ppl
Rob Salomone’s course is excellent and starts with great examples.
Jan-Willem van de Meent, Brooks Paige, Hongseok Yang, Frank Wood, An Introduction to Probabilistic Programming
Richard McElreath, Statistical Rethinking has gone viral as an introduction to some of these ideas. It is available on O’Reilly (free for CSIRO people). There is PyMC3 and a numpyro version.
Kevin Murphy’s probml/pml-book: Probabilistic Machine Learning
Wi Ji Ma, Konrad Paul Kording, Daniel Goldreich, Bayesian models of perception and action
Noah D. Goodman, Joshua B. Tenenbaum et al., Probabilistic Models of Cognition - 2nd Edition
Noah D. Goodman and Andreas Stuhlmüller, The Design and Implementation of Probabilistic Programming Languages
Barber (2012)
Bishop (2006)
1.1 MCMC considerations
Maybe see MCMC for now.
1.2 Variational inference considerations
Maybe see variational inference for now.
2 Toolkits
There are too many PPLs. I’ve actually played with some of them, and they’re documented below.
2.1 Pyro
pytorch + bayes = pyro. (Pradhan et al. 2018)
Pyro is a workhorse tool at the moment, so it now gets its own notebook.
2.2 Stan
Stan is the solid default inference toolbox. If Stan can handle your problem, it’s a convenient and well-documented option.
Stan breaks down in some circumstances. It doesn’t express neural-network models naturally, and we have reason to worry that the posterior simulations will be nasty with very high-dimensional parameter vectors.
Stan does support some variational inference, not just Monte Carlo sampling. However, last time I checked (2017) the variational features weren’t flexible enough to be useful for me and were not recommended.
See the Stan notebook.
2.3 Mici
Mici doesn’t do everything in probabilistic programming, but it does HMC sampling if you have a log pdf.
Mici is a Python package providing implementations of Markov chain Monte Carlo (MCMC) methods for approximate inference in probabilistic models, with a particular focus on MCMC methods based on simulating Hamiltonian dynamics on a manifold.
Key features include
- a modular design allowing use of a wide range of inference algorithms by mixing and matching different components, and making it easy to extend the package,
- a pure Python code base with minimal dependencies, allowing easy integration within other code,
- implementations of MCMC methods for sampling from distributions on embedded manifolds implicitly-defined by a constraint equation and distributions on Riemannian manifolds with a user-specified metric,
- computationally efficient inference via transparent caching of the results of expensive operations and intermediate results calculated in derivative computations allowing later reuse without recalculation,
- memory efficient inference for large models by memory-mapping chains to disk, allowing long runs on large models without hitting memory issues.
2.4 BlackJAX
Like Mici, BlackJAX doesn’t cover the whole probabilistic programming space, but it provides HMC sampling if we have a log‑pdf.
BlackJAX should appeal to those who:
- Have a logpdf and just need a sampler;
- Need more than a general-purpose sampler;
- Want to sample on GPU;
- Want to build upon robust elementary blocks for their research;
- Are building a probabilistic programming language;
- Want to learn how sampling algorithms work.
3 Oryx
- jax-ml/oryx: Oryx is a library for probabilistic programming and deep learning built on top of JAX.
- Oryx | TensorFlow
3.1 ForneyLab.jl
Seems to have gone very hardcore on variational message passing (van de Laar et al. 2018; Akbayrak, Bocharov, and de Vries 2021).
3.2 Turing.jl
Turing.jlis a Julia library for (universal) probabilistic programming. Current features include:
- Universal probabilistic programming with an intuitive modelling interface
- Hamiltonian Monte Carlo (HMC) sampling for differentiable posterior distributions
- Particle MCMC sampling for complex posterior distributions involving discrete variables and stochastic control flows
- Gibbs sampling that combines particle MCMC and HMC
This is one of many Julia options and includes an MCMC toolkit AdvancedHMC.jl.
3.3 ProbFlow
3.4 Oryx
Oryx is a library for probabilistic programming and deep learning built on top of JAX.
Oryx’s approach is to expose a set of function transformations that compose and integrate with JAX’s existing transformations.
It seems slightly magical; check out their opening example:
3.5 Gen
Gen:
Gensimplifies the use of probabilistic modeling and inference, by providing modeling languages in which users express models, and high-level programming constructs that automate aspects of inference.Like some probabilistic programming research languages, Gen includes universal modeling languages that can represent any model, including models with stochastic structure, discrete and continuous random variables, and simulators. However, Gen is distinguished by the flexibility that it affords to users for customising their inference algorithm.
Gen’s flexible modeling and inference programming capabilities unify symbolic, neural, probabilistic, and simulation-based approaches to modeling and inference, including causal modeling, symbolic programming, deep learning, hierarchical Bayesian modeling, graphics and physics engines, and planning and reinforcement learning.
It has an impressive talk demonstrating how we would interactively clean data using it.
3.6 Edward/Edward2
From Blei’s lab, it leverages trendy deep learning machinery, TensorFlow for variational Bayes and such.
This is now baked into TensorFlow as a probabilistic programming interface. I don’t use it because I don’t trust TensorFlow, and anyway everyone at Google seems to use JAX instead.
3.7 TensorFlow Probability
Another TensorFlow entrant. It’s low-level and messy. Edward2 (above) uses it, but it’s presumably more basic. The precise relationships between these TensorFlow things are complicated enough that it’s a whole other research project to pick them apart.
3.8 pyprob
pyprob: (Le, Baydin, and Wood 2017)
pyprob is a PyTorch-based library for probabilistic programming and inference compilation. The main focus of this library is on coupling existing simulation codebases with probabilistic inference with minimal intervention.
The main advantage of pyprob, compared against other probabilistic programming languages like Pyro, is a fully automatic amortised inference procedure based on importance sampling. pyprob only requires a generative model to be specified. Particularly, pyprob allows for efficient inference using inference compilation which trains a recurrent neural network as a proposal network.
In Pyro such an inference network requires the user to explicitly define the control flow of the network, which is due to Pyro running the inference network and generative model sequentially. However, in pyprob the generative model and inference network runs concurrently. Thus, the control flow of the model is directly used to train the inference network. This alleviates the need for manually defining its control flow.
The flagship application appears to be etalumis (Baydin et al. 2019) a framework that, as far as I can tell, emphasizes Bayesian inverse problems.
3.9 PyMC3
The PyMC family has produced many probabilistic programming ideas, blog posts and code since the mid 2000s. They’re an excellent place to learn probabilistic programming, although not the best source of stable, finished products, even by the field’s mercurial standards.
PyMC3 is Python+Theano, although they have ported Theano to JAX and renamed it Aesara. They claim this is fast and it might be an easy way to access JAX-accelerated sampling if Numpyro feels too exhausting. 1
See Chris Fonnesbeck’s example in Python.
Thomas Wiecki’s Bayesian Deep Learning demonstrates some variants with PyMC3.
3.10 Aesara PPL
3.11 Mamba.jl
Mamba is an open platform for the implementation and application of MCMC methods to perform Bayesian analysis in Julia. The package provides a framework for (1) specification of hierarchical models through stated relationships between data, parameters, and statistical distributions; (2) block-updating of parameters with samplers provided, defined by the user, or available from other packages; (3) execution of sampling schemes; and (4) posterior inference. It is intended to give users access to all levels of the design and implementation of MCMC simulators to particularly aid in the development of new methods.
Several software options are available for MCMC sampling of Bayesian models. Individuals who are primarily interested in data analysis, unconcerned with the details of MCMC, and have models that can be fit in JAGS, Stan, or OpenBUGS are encouraged to use those programs. Mamba is intended for individuals who wish to have access to lower-level MCMC tools, are knowledgeable of MCMC methodologies, and have experience, or wish to gain experience, with their application. The package also provides stand-alone convergence diagnostics and posterior inference tools, which are essential for the analysis of MCMC output regardless of the software used to generate it.
3.12 Greta
greta models are written right in R, so there’s no need to learn another language like BUGS or Stan
greta uses Google TensorFlow
I wonder how it uses Google’s TensorFlow.
3.13 Soss.jl
Soss is a library for probabilistic programming.
Let’s jump right in with a simple linear model:
In Soss, models are first-class and function-like, and “applying” a model to its arguments gives a joint distribution.
Just a few of the things we can do in Soss:
- Sample from the (forward) model
- Condition a joint distribution on a subset of parameters
- Have arbitrary Julia values (yes, even other models) as inputs or outputs of a model
- Build a new model for the predictive distribution, for assigning parameters to particular values
How does it do all these things exactly?
3.14 Miscellaneous Julia options
DynamicHMC.jl It does Hamiltonian/NUTS sampling in a raw-likelihood setting.
Miletus is a financial product and term-structure modelling package that is available for quant work in Julia as part of the paid packages offerings in finance. Although it looks like it’s also freely available?
3.15 Inferpy
InferPy It seems to be a higher-level competitor to Edward2?
3.16 Zhusuan
ZhuSuan is a Python probabilistic programming library for Bayesian deep learning, which conjoins the complementary advantages of Bayesian methods and deep learning. ZhuSuan is built upon TensorFlow. Unlike existing deep learning libraries, which are mainly designed for deterministic neural networks and supervised tasks, ZhuSuan provides deep learning style primitives and algorithms for building probabilistic models and applying Bayesian inference. The supported inference algorithms include:
- Variational inference with programmable variational posteriors, various objectives and advanced gradient estimators (SGVB, REINFORCE, VIMCO, etc).
- Importance sampling for learning and evaluating models, with programmable proposals.
- Hamiltonian Monte Carlo (HMC) with parallel chains, and optional automatic parameter tuning.
3.17 Church/Anglican
Church is a general-purpose Turing-complete Monte Carlo Lisp derivative that’s unbearably slow but pulls some reputedly cute tricks with modelling human problem-solving and other likelihood-free methods, according to its creators, Noah Goodman and Joshua Tenenbaum.
See also Anglican, which is the same but different — it’s built in Clojure and so it also leverages browser ClojureScript.
3.18 WebPPL
WebPPL is a successor to Church, designed as a teaching language for probabilistic reasoning in the browser. If we like JavaScript ML.
3.19 BAT
See also BAT, the Bayesian Analysis Toolkit, which does sophisticated Bayes modelling, although AFAICT it uses a fairly basic Metropolis–Hastings sampler.
4 Incoming
ArviZ is a Python package for exploratory analysis of Bayesian models. Includes functions for posterior analysis, data storage, sample diagnostics, model checking, and comparison.
The goal is to provide backend-agnostic tools for diagnostics and visualizations of Bayesian inference in Python, by first converting inference data into xarray objects. See here for more on xarray and ArviZ usage and here for more on
InferenceDatastructure and specification.
5 References
Footnotes
Beware: PyMC4, despite what you might think from the jetsam of an earlier hype cycle, is discontinued in favour of PyMC3. As far as I can tell PyMC4 was intended to be a TensorFlow-backed system, so this is further evidence that TensorFlow blights every probabilistic programming system it touches.↩︎